gamma correction for lcd monitors price

Problems like extremely poor display of shadow areas, blown-out highlights, or images prepared on Macs appearing too dark on Windows computers are often due to gamma characteristics. In this session, we"ll discuss gamma, which has a significant impact on color reproduction on LCD monitors. Understanding gamma is useful in both color management and product selection. Users who value picture quality are advised to check this information.

* Below is the translation from the Japanese of the ITmedia article "Is the Beauty of a Curve Decisive for Color Reproduction? Learning About LCD Monitor Gamma" published July 13, 2009. Copyright 2011 ITmedia Inc. All Rights Reserved.

The term gamma comes from the third letter of the Greek alphabet, written Γ in upper case and γ in lower case. The word gamma occurs often in everyday life, in terms like gamma rays, the star called Gamma Velorum, and gamma-GTP. In computer image processing, the term generally refers to the brightness of intermediate tones (gray).

Let"s discuss gamma in a little more detail. In a PC environment, the hardware used when working with color includes monitors, printers, and scanners. When using these devices connected to a PC, we input and output color information to and from each device. Since each device has its own unique color handling characteristics (or tendencies), color information cannot be output exactly as input. The color handling characteristics that arise in input and output are known as gamma characteristics.

While certain monitors are also compatible with color handling at 10 bits per RGB color (210 = 1024 tones), or 1024 x 3 (approximately 1,064,330,000 colors), operating system and application support for such monitors has lagged. Currently, some 16.77 million colors, with eight bits per RGB color, is the standard color environment for PC monitors.

When a PC and a monitor exchange color information, the ideal is a relationship in which the eight-bit color information per RGB color input from the PC to the monitor can be output accurately—that is, a 1:1 relationship for input:output. However, since gamma characteristics differ between PCs and monitors, color information is not transmitted according to a 1:1 input:output relationship.

How colors ultimately look depends on the relationship resulting from the gamma values (γ) that numerically represent the gamma characteristics of each hardware device. If the color information input is represented as x and output as y, the relationship applying the gamma value can be represented by the equation y = xγ.

Gamma characteristics are represented by the equation y = xγ. At the ideal gamma value of 1.0, y = x; but since each monitor has its own unique gamma characteristics (gamma values), y generally doesn"t equal x. The above graph depicts a curve adjusted to the standard Windows gamma value of 2.2. The standard gamma value for the Mac OS is 1.8.

Ordinarily, the nature of monitor gamma is such that intermediate tones tend to appear dark. Efforts seek to promote accurate exchange of color information by inputting data signals in which the intermediate tones have already been brightened to approach an input:output balance of 1:1. Balancing color information to match device gamma characteristics in this way is called gamma correction.

A simple gamma correction system. If we account for monitor gamma characteristics and input color information with gamma values adjusted accordingly (i.e., color information with intermediate tones brightened), color handling approaches the y = x ideal. Since gamma correction generally occurs automatically, users usually obtain correct color handling on a PC monitor without much effort. However, the precision of gamma correction varies from manufacturer to manufacturer and from product to product (see below for details).

In most cases, if a computer runs the Windows operating system, we can achieve close to ideal colors by using a monitor with a gamma value of 2.2. This is because Windows assumes a monitor with a gamma value of 2.2, the standard gamma value for Windows. Most LCD monitors are designed based on a gamma value of 2.2.

The standard monitor gamma value for the Mac OS is 1.8. The same concept applies as in Windows. We can obtain color reproduction approaching the ideal by connecting a Mac to a monitor configured with a gamma value of 1.8.

An example of the same image displayed at gamma values of 2.2 (photo at left) and 1.8 (photo at right). At a gamma value of 1.8, the overall image appears brighter. The LCD monitor used is EIZO"s 20-inch wide-screen EV2023W FlexScan model (ITmedia site).

To equalize color handling in mixed Windows and Mac environments, it"s a good idea to standardize the gamma values between the two operating systems. Changing the gamma value for the Mac OS is easy; but Windows provides no such standard feature. Since Windows users perform color adjustments through the graphics card driver or separate color-adjustment software, changing the gamma value can be an unexpectedly complex task. If the monitor used in a Windows environment offers a feature for adjusting gamma values, obtaining more accurate results will likely be easier.

If we know that a certain image was created in a Mac OS environment with a gamma value of 1.8, or if an image received from a Mac user appears unnaturally dark, changing the monitor gamma setting to 1.8 should show the image with the colors intended by the creator.

Eizo Nanao"s LCD monitors allow users to configure the gamma value from the OSD menu, making this procedure easy. In addition to the initially configured gamma value of 2.2., one can choose from multiple settings, including the Mac OS standard of 1.8.

To digress slightly, standard gamma values differ between Windows and Mac OS for reasons related to the design concepts and histories of the two operating systems. Windows adopted a gamma value corresponding to television (2.2), while the Mac OS adopted a gamma value corresponding to commercial printers (1.8). The Mac OS has a long history of association with commercial printing and desktop publishing applications, for which 1.8 remains the basic gamma value, even now. On the other hand, a gamma value of 2.2 is standard in the sRGB color space, the standard for the Internet and for digital content generally, and for Adobe RGB, the use of which has expanded for wide-gamut printing,.

Given the proliferating use of color spaces like sRGB and Adobe RGB, plans call for the latest Mac OS scheduled for release by Apple Computer in September 2009, Mac OS X 10.6 Snow Leopard, to switch from a default gamma value of 1.8 to 2.2. A gamma value of 2.2 is expected to become the future mainstream for Macs.

On the preceding page, we mentioned that the standard gamma value in a Windows environment is 2.2 and that many LCD monitors can be adjusted to a gamma value of 2.2. However, due to the individual tendencies of LCD monitors (or the LCD panels installed in them), it"s hard to graph a smooth gamma curve of 2.2.

Traditionally, LCD panels have featured S-shaped gamma curves, with ups and downs here and there and curves that diverge by RGB color. This phenomenon is particularly marked for dark and light tones, often appearing to the eye of the user as tone jumps, color deviations, and color breakdown.

The internal gamma correction feature incorporated into LCD monitors that emphasize picture quality allows such irregularity in the gamma curve to be corrected to approach the ideal of y = x γ. Device specs provide one especially useful figure to help us determine whether a monitor has an internal gamma correction feature: A monitor can be considered compatible with internal gamma correction if the figure for maximum number of colors is approximately 1,064,330,000 or 68 billion or if the specs indicate the look-up table (LUT) is 10- or 12-bit.

An internal gamma correction feature applies multi-gradation to colors and reallocates them. While the input from a PC to an LCD monitor is in the form of color information at eight bits per RGB color, within the LCD monitor, multi-gradation is applied to increase this to 10 bits (approximately 1,064,330,000 colors) or 12 bits (approximately 68 billion colors). The optimal color at eight bits per RGB color (approximately 16.77 million colors) is identified by referring to the LUT and displayed on screen. This corrects irregularity in the gamma curve and deviations in each RGB color, causing the output on screen to approach the ideal of y = x γ.

Let"s look at a little more information on the LUT. The LUT is a table containing the results of certain calculations performed in advance. The results for certain calculations can be obtained simply by referring to the LUT, without actually performing the calculations. This accelerates processing and reduces the load on a system. The LUT in an LCD monitor identifies the optimal eight-bit RGB colors from multi-gradation color data of 10 or more bits.

An overview of an internal gamma correction feature. Eight-bit RGB color information input from the PC is subjected to multi-gradation to 10 or more bits. This is then remapped to the optimal eight-bit RGB tone by referring to the LUT. Following internal gamma correction, the results approach the ideal gamma curve, dramatically improving on screen gradation and color reproduction.

Eizo Nanao"s LCD monitors proactively employ internal gamma correction features. In models designed especially for high picture quality and in some models in the ColorEdge series designed for color management, eight-bit RGB input signals from the PC are subjected to multi-gradation, and calculations are performed at 14 or 16 bits. A key reason for performing calculations at bit counts higher than the LUT bit count is to improve gradation still further, particularly the reproduction of darker tones. Users seeking high-quality color reproduction should probably choose a monitor model like this one.

In conclusion, we"ve prepared image patterns that make it easy to check the gamma values of an LCD monitor, based on this session"s discussion. Looking directly at your LCD monitor, move back slightly from the screen and gaze at the following images with your eyes half-closed. Visually compare the square outlines and the stripes around them, looking for patterns that appear to have the same tone of gray (brightness). The pattern for which the square frame and the striped pattern around it appear closest in brightness represents the rough gamma value to which the monitor is currently configured.

Based on a gamma value of 2.2, if the square frame appears dark, the LCD monitor"s gamma value is low. If the square frame appears bright, the gamma value is high. You can adjust the gamma value by changing the LCD monitor"s brightness settings or by adjusting brightness in the driver menu for the graphics card.

Naturally, it"s even easier to adjust the gamma if you use a model designed for gamma value adjustments, like an EIZO LCD monitor. For even better color reproduction, you can set the gamma value and optimize color reproduction by calibrating your monitor.

The effect of gamma correction on an image: The original image was taken to varying powers, showing that powers larger than 1 make the shadows darker, while powers smaller than 1 make dark regions lighter.

Gamma correction or gamma is a nonlinear operation used to encode and decode luminance or tristimulus values in video or still image systems.power-law expression:

Gamma encoding of images is used to optimize the usage of bits when encoding an image, or bandwidth used to transport an image, by taking advantage of the non-linear manner in which humans perceive light and color.lightness), under common illumination conditions (neither pitch black nor blindingly bright), follows an approximate power function (which has no relation to the gamma function), with greater sensitivity to relative differences between darker tones than between lighter tones, consistent with the Stevens power law for brightness perception. If images are not gamma-encoded, they allocate too many bits or too much bandwidth to highlights that humans cannot differentiate, and too few bits or too little bandwidth to shadow values that humans are sensitive to and would require more bits/bandwidth to maintain the same visual quality.floating-point images is not required (and may be counterproductive), because the floating-point format already provides a piecewise linear approximation of a logarithmic curve.

Although gamma encoding was developed originally to compensate for the input–output characteristic of cathode ray tube (CRT) displays, it is not its main purpose or advantage in modern systems. In CRT displays, the light intensity varies nonlinearly with the electron-gun voltage. Altering the input signal by gamma compression can cancel this nonlinearity, such that the output picture has the intended luminance. However, the gamma characteristics of the display device do not play a factor in the gamma encoding of images and video. They need gamma encoding to maximize the visual quality of the signal, regardless of the gamma characteristics of the display device.

Analogously, digital cameras record light using electronic sensors that usually respond linearly. In the process of rendering linear raw data to conventional RGB data (e.g. for storage into JPEG image format), color space transformations and rendering transformations will be performed. In particular, almost all standard RGB color spaces and file formats use a non-linear encoding (a gamma compression) of the intended intensities of the primary colors of the photographic reproduction. In addition, the intended reproduction is almost always nonlinearly related to the measured scene intensities, via a tone reproduction nonlinearity.

That is, gamma can be visualized as the slope of the input–output curve when plotted on logarithmic axes. For a power-law curve, this slope is constant, but the idea can be extended to any type of curve, in which case gamma (strictly speaking, "point gamma"

When a photographic film is exposed to light, the result of the exposure can be represented on a graph showing log of exposure on the horizontal axis, and density, or negative log of transmittance, on the vertical axis. For a given film formulation and processing method, this curve is its characteristic or Hurter–Driffield curve.

Output to CRT-based television receivers and monitors does not usually require further gamma correction. The standard video signals that are transmitted or stored in image files incorporate gamma compression matching the gamma expansion of the CRT (although it is not the exact inverse).

For television signals, gamma values are fixed and defined by the analog video standards. CCIR System M and N, associated with NTSC color, use gamma 2.2; the rest (systems B/G, H, I, D/K, K1 and L) associated with PAL or SECAM color, use gamma 2.8.

In most computer display systems, images are encoded with a gamma of about 0.45 and decoded with the reciprocal gamma of 2.2. A notable exception, until the release of Mac OS X 10.6 (Snow Leopard) in September 2009, were Macintosh computers, which encoded with a gamma of 0.55 and decoded with a gamma of 1.8. In any case, binary data in still image files (such as JPEG) are explicitly encoded (that is, they carry gamma-encoded values, not linear intensities), as are motion picture files (such as MPEG). The system can optionally further manage both cases, through color management, if a better match to the output device gamma is required.

Plot of the sRGB standard gamma-expansion nonlinearity in red, and its local gamma value (slope in log–log space) in blue. The local gamma rises from 1 to about 2.2.

The sRGB color space standard used with most cameras, PCs, and printers does not use a simple power-law nonlinearity as above, but has a decoding gamma value near 2.2 over much of its range, as shown in the plot to the right. Below a compressed value of 0.04045 or a linear intensity of 0.00313, the curve is linear (encoded value proportional to intensity), so γ = 1. The dashed black curve behind the red curve is a standard γ = 2.2 power-law curve, for comparison.

Gamma correction in computers is used, for example, to display a gamma = 1.8 Apple picture correctly on a gamma = 2.2 PC monitor by changing the image gamma. Another usage is equalizing of the individual color-channel gammas to correct for monitor discrepancies.

Some picture formats allow an image"s intended gamma (of transformations between encoded image samples and light output) to be stored as metadata, facilitating automatic gamma correction as long as the display system"s exponent is known. The PNG specification includes the gAMA chunk for this purposeJPEG and TIFF the Exif Gamma tag can be used.

These features have historically caused problems, especially on the web. There is no numerical value of gamma that matches the "show the 8-bit numbers unchanged" method used for JPG, GIF, HTML, and CSS colors, so the PNG would not match.Google Chrome (and all other Chromium-based browsers) and Mozilla Firefox either ignore the gamma setting entirely, or ignore it when set to known wrong values.

A gamma characteristic is a power-law relationship that approximates the relationship between the encoded luma in a television system and the actual desired image luminance.

With this nonlinear relationship, equal steps in encoded luminance correspond roughly to subjectively equal steps in brightness. Ebner and Fairchildused an exponent of 0.43 to convert linear intensity into lightness (luma) for neutrals; the reciprocal, approximately 2.33 (quite close to the 2.2 figure cited for a typical display subsystem), was found to provide approximately optimal perceptual encoding of grays.

The following illustration shows the difference between a scale with linearly-increasing encoded luminance signal (linear gamma-compressed luma input) and a scale with linearly-increasing intensity scale (linear luminance output).

On most displays (those with gamma of about 2.2), one can observe that the linear-intensity scale has a large jump in perceived brightness between the intensity values 0.0 and 0.1, while the steps at the higher end of the scale are hardly perceptible. The gamma-encoded scale, which has a nonlinearly-increasing intensity, will show much more even steps in perceived brightness.

A cathode ray tube (CRT), for example, converts a video signal to light in a nonlinear way, because the electron gun"s intensity (brightness) as a function of applied video voltage is nonlinear. The light intensity I is related to the source voltage Vs according to

where γ is the Greek letter gamma. For a CRT, the gamma that relates brightness to voltage is usually in the range 2.35 to 2.55; video look-up tables in computers usually adjust the system gamma to the range 1.8 to 2.2,

For simplicity, consider the example of a monochrome CRT. In this case, when a video signal of 0.5 (representing a mid-gray) is fed to the display, the intensity or brightness is about 0.22 (resulting in a mid-gray, about 22% the intensity of white). Pure black (0.0) and pure white (1.0) are the only shades that are unaffected by gamma.

To compensate for this effect, the inverse transfer function (gamma correction) is sometimes applied to the video signal so that the end-to-end response is linear. In other words, the transmitted signal is deliberately distorted so that, after it has been distorted again by the display device, the viewer sees the correct brightness. The inverse of the function above is

where Vc is the corrected voltage, and Vs is the source voltage, for example, from an image sensor that converts photocharge linearly to a voltage. In our CRT example 1/γ is 1/2.2 ≈ 0.45.

A color CRT receives three video signals (red, green, and blue) and in general each color has its own value of gamma, denoted γR, γG or γB. However, in simple display systems, a single value of γ is used for all three colors.

Other display devices have different values of gamma: for example, a Game Boy Advance display has a gamma between 3 and 4 depending on lighting conditions. In LCDs such as those on laptop computers, the relation between the signal voltage Vs and the intensity I is very nonlinear and cannot be described with gamma value. However, such displays apply a correction onto the signal voltage in order to approximately get a standard γ = 2.5 behavior. In NTSC television recording, γ = 2.2.

The power-law function, or its inverse, has a slope of infinity at zero. This leads to problems in converting from and to a gamma colorspace. For this reason most formally defined colorspaces such as sRGB will define a straight-line segment near zero and add raising x + K (where K is a constant) to a power so the curve has continuous slope. This straight line does not represent what the CRT does, but does make the rest of the curve more closely match the effect of ambient light on the CRT. In such expressions the exponent is not the gamma; for instance, the sRGB function uses a power of 2.4 in it, but more closely resembles a power-law function with an exponent of 2.2, without a linear portion.

Up to four elements can be manipulated in order to achieve gamma encoding to correct the image to be shown on a typical 2.2- or 1.8-gamma computer display:

The pixel"s intensity values in a given image file; that is, the binary pixel values are stored in the file in such way that they represent the light intensity via gamma-compressed values instead of a linear encoding. This is done systematically with digital video files (as those in a DVD movie), in order to minimize the gamma-decoding step while playing, and maximize image quality for the given storage. Similarly, pixel values in standard image file formats are usually gamma-compensated, either for sRGB gamma (or equivalent, an approximation of typical of legacy monitor gammas), or according to some gamma specified by metadata such as an ICC profile. If the encoding gamma does not match the reproduction system"s gamma, further correction may be done, either on display or to create a modified image file with a different profile.

The rendering software writes gamma-encoded pixel binary values directly to the video memory (when highcolor/truecolor modes are used) or in the CLUT hardware registers (when indexed color modes are used) of the display adapter. They drive Digital-to-Analog Converters (DAC) which output the proportional voltages to the display. For example, when using 24-bit RGB color (8 bits per channel), writing a value of 128 (rounded midpoint of the 0–255 byte range) in video memory it outputs the proportional ≈ 0.5 voltage to the display, which it is shown darker due to the monitor behavior. Alternatively, to achieve ≈ 50% intensity, a gamma-encoded look-up table can be applied to write a value near to 187 instead of 128 by the rendering software.

Modern display adapters have dedicated calibrating CLUTs, which can be loaded once with the appropriate gamma-correction look-up table in order to modify the encoded signals digitally before the DACs that output voltages to the monitor.hardware calibration.

Some modern monitors allow the user to manipulate their gamma behavior (as if it were merely another brightness/contrast-like setting), encoding the input signals by themselves before they are displayed on screen. This is also a calibration by hardware technique but it is performed on the analog electric signals instead of remapping the digital values, as in the previous cases.

In a typical system, for example from camera through JPEG file to display, the role of gamma correction will involve several cooperating parts. The camera encodes its rendered image into the JPEG file using one of the standard gamma values such as 2.2, for storage and transmission. The display computer may use a color management engine to convert to a different color space (such as older Macintosh"s γ = 1.8 color space) before putting pixel values into its video memory. The monitor may do its own gamma correction to match the CRT gamma to that used by the video system. Coordinating the components via standard interfaces with default standard gamma values makes it possible to get such system properly configured.

This procedure is useful for making a monitor display images approximately correctly, on systems in which profiles are not used (for example, the Firefox browser prior to version 3.0 and many others) or in systems that assume untagged source images are in the sRGB colorspace.

In the test pattern, the intensity of each solid color bar is intended to be the average of the intensities in the surrounding striped dither; therefore, ideally, the solid areas and the dithers should appear equally bright in a system properly adjusted to the indicated gamma.

Normally a graphics card has contrast and brightness control and a transmissive LCD monitor has contrast, brightness, and backlight control. Graphics card and monitor contrast and brightness have an influence on effective gamma, and should not be changed after gamma correction is completed.

Given a desired display-system gamma, if the observer sees the same brightness in the checkered part and in the homogeneous part of every colored area, then the gamma correction is approximately correct.

Before gamma correction the desired gamma and color temperature should be set using the monitor controls. Using the controls for gamma, contrast and brightness, the gamma correction on an LCD can only be done for one specific vertical viewing angle, which implies one specific horizontal line on the monitor, at one specific brightness and contrast level. An ICC profile allows one to adjust the monitor for several brightness levels. The quality (and price) of the monitor determines how much deviation of this operating point still gives a satisfactory gamma correction. Twisted nematic (TN) displays with 6-bit color depth per primary color have lowest quality. In-plane switching (IPS) displays with typically 8-bit color depth are better. Good monitors have 10-bit color depth, have hardware color management and allow hardware calibration with a tristimulus colorimeter. Often a 6bit plus FRC panel is sold as 8bit and a 8bit plus FRC panel is sold as 10bit. FRC is no true replacement for more bits. The 24-bit and 32-bit color depth formats have 8 bits per primary color.

With Microsoft Windows 7 and above the user can set the gamma correction through the display color calibration tool dccw.exe or other programs.ICC profile file and load it as default. This makes color management easy.color Look Up Table correctly after waking up from standby or hibernate mode and show wrong gamma. In this case update the graphics card driver.

On some operating systems running the X Window System, one can set the gamma correction factor (applied to the existing gamma value) by issuing the command xgamma -gamma 0.9 for setting gamma correction factor to 0.9, and xgamma for querying current value of that factor (the default is 1.0). In macOS systems, the gamma and other related screen calibrations are made through the System Preferences.

The test image is only valid when displayed "raw", i.e. without scaling (1:1 pixel to screen) and color adjustment, on the screen. It does, however, also serve to point out another widespread problem in software: many programs perform scaling in a color space with gamma, instead of a physically-correct linear space. In a sRGB color space with an approximate gamma of 2.2, the image should show a "2.2" result at 50% size, if the zooming is done linearly. Jonas Berlin has created a "your scaling software sucks/rules" image based on the same principle.

In addition to scaling, the problem also applies to other forms of downsampling (scaling down), such as chroma subsampling in JPEG"s gamma-enabled Y′CbCr.WebP solves this problem by calculating the chroma averages in linear space then converting back to a gamma-enabled space; an iterative solution is used for larger images. The same "sharp YUV" (formerly "smart YUV") code is used in sjpeg. Kornelski provides a simpler approximation by luma-based weighted average.Alpha compositing, color gradients, and 3D rendering are also affected by this issue.

Paradoxically, when upsampling (scaling up) an image, the result processed in the "wrong" gamma-enabled space tends to be more aesthetically pleasing. This is because upscaling filters are tuned to minimize the ringing artifacts in a linear space, but human perception is non-linear and better approximated by gamma. An alternative way to trim the artifacts is using a sigmoidal light transfer function, a technique pioneered by GIMP"s LoHalo filter and later adopted by madVR.

The term intensity refers strictly to the amount of light that is emitted per unit of time and per unit of surface, in units of lux. Note, however, that in many fields of science this quantity is called luminous exitance, as opposed to luminous intensity, which is a different quantity. These distinctions, however, are largely irrelevant to gamma compression, which is applicable to any sort of normalized linear intensity-like scale.

One contrasts relative luminance in the sense of color (no gamma compression) with luma in the sense of video (with gamma compression), and denote relative luminance by Y and luma by Y′, the prime symbol (′) denoting gamma compression.

Gamma correction is a type of power law function whose exponent is the Greek letter gamma (γ). It should not be confused with the mathematical Gamma function. The lower case gamma, γ, is a parameter of the former; the upper case letter, Γ, is the name of (and symbol used for) the latter (as in Γ(x)). To use the word "function" in conjunction with gamma correction, one may avoid confusion by saying "generalized power law function".

Without context, a value labeled gamma might be either the encoding or the decoding value. Caution must be taken to correctly interpret the value as that to be applied-to-compensate or to be compensated-by-applying its inverse. In common parlance, in many occasions the decoding value (as 2.2) is employed as if it were the encoding value, instead of its inverse (1/2.2 in this case), which is the real value that must be applied to encode gamma.

McKesson, Jason L. "Chapter 12. Dynamic Range – Linearity and Gamma". Learning Modern 3D Graphics Programming. Archived from the original on 18 July 2013. Retrieved 11 July 2013.

"11A: Characteristics of systems for monochrome and color television". Reports of the CCIR, 1990: Also Decisions : XVIIth Plenary Assembly, Dusseldorf (PDF). International Radio Consultative Committee. 1990.

Fritz Ebner and Mark D Fairchild, "Development and testing of a color space (IPT) with improved hue uniformity," Proceedings of IS&T/SID"s Sixth Color Imaging Conference, p 8-13 (1998).

Koren, Norman. "Monitor calibration and gamma". Retrieved 2018-12-10. The chart below enables you to set the black level (brightness) and estimate display gamma over a range of 1 to 3 with precison better than 0.1.

Nienhuys, Han-Kwang (2008). "Gamma calibration". Retrieved 2018-11-30. The reason for using 48% rather than 50% as a luminance is that many LCD screens have saturation issues in the last 5 percent of their brightness range that would distort the gamma measurement.

Andrews, Peter. "The Monitor calibration and Gamma assessment page". Retrieved 2018-11-30. the problem is caused by the risetime of most monitor hardware not being sufficiently fast to turn from full black to full white in the space of a single pixel, or even two, in some cases.

Werle, Eberhard. "Quickgamma". Retrieved 2018-12-10. QuickGamma is a small utility program to calibrate a monitor on the fly without having to buy expensive hardware tools.

The Levels center slider is a multiplier of the current image gamma. I don"t find that "multiplier" written about so much any more, but it was popular, widely known and discussed 15-20 years ago (CRT days, back when we knew what gamma was). Gamma used to be very important, but today, we still encode with 1/2.2, and the LCD monitor must decode with 2.2, and for an LCD monitor, gamma is just an automatic no-op now (printers and CRT still make use of it).

Evidence of the tool as multiplier: An eyedropper on the gray road at the curve ahead in the middle image at gamma 2.2 reads 185 (I"m looking at the red value). Gamma 2.2 puts that linear value at 126 (midscale). 126 at gamma 1 is 126 (measured in top image, 0.45x x 2.2 = gamma 1). 126 at gamma 4.8 is 220 (measured in bottom image, 2.2x x 2.2 = gamma 4.8). Q.E.D.

Today, our LCD display is considered linear and technically does not need gamma. However we still necessarily continue gamma to provide compatibility with all the world"s previous images and video systems, and for CRT and printers too. The LCD display simply uses a chip (LookUp table, next page) to decode it first (discarding gamma correction to necessarily restore the original linear image). Note that gamma is a Greek letter used for many variables in science (like X is used in algebra, used many ways), so there are also several other unrelated uses of the word gamma, in math and physics, or for film contrast, etc, but all are different unrelated concepts. For digital images, the use of the term gamma is to describe the CRT response curve.

We must digitize an image first to show it on our computer video system. But all digital cameras and scanners always automatically add gamma to all tonal images. By "tonal", I mean a color or grayscale image is tonal (has many different tones), as opposed to a one-bit line art image (two colors, black or white, 0 or 1, which has no gray tones, like clip art or fax) does not need or get gamma (values 0 and 1 are entirely unaffected by gamma).

Gamma correction is automatically done to any image from by any digital camera (still or movie), and from any scanner, or created in graphic editors... any digital tonal image that might be created in any way. A raw image is an exception, only because then gamma is deferred until later when it actually becomes a RGB image. Gamma is an invisible background process, and we don"t have to necessarily be aware of it, it just always happens. This does mean that all of our image histograms contain and show gamma data. The 128 value that we may think of as midscale is not middle tone of the histograms we see. This original linear 128 middle value (middle at 50% linear data, 1 stop down from 255) is up at about 186 in gamma data, and in our histograms.

The reason we use gamma correction. For many years, CRT was the only video display we had (other than projecting film). But CRT is not linear, and requires heroic efforts to properly use them for tonal images (photos and TV). The technical reason we needed gamma is that the CRT light beam intensity efficiency varies with the tubes electron gun signal voltage. CRT does not use the decode formula, which simply resulted from the study of what the non-linear CRT losses already actually do in the act of showing it on a CRT ... the same effect. The non-linear CRT simply shows the tones, with the response is sort of as if the numeric values were squared first (2.2 is near 2). These losses have variable results, depending on the tones value, but the brighter values are brighter, and the darker values are darker. Not linear.

How does CRT Gamma Correction actually do its work? Gamma 2.2 is roughly 2, so there"s only a small difference from 1/2 square root, and 2 squared. I hope that approximation simplifies instead of confusing. So Encoding Gamma Correction input to the power of 1/2.2 is roughly the square root, which condenses the image gamma data range smaller. Then later, CRT Gamma Decodes it to power of 2.2, roughly squared, which expands it to bring it back exactly to the original value (reversible). Specifically, for a numerical example for two tones 225 and 25, value 225 is 9x brighter then 25 (225/25=9). But (using easier exponent 2 instead of 2.2), the square roots are 15 and 5, which is only 3 times more then, compressed together, much less difference ... 3² is 9 (and if we use 2.2, then 2.7 times more). So in that way, gamma correction data boosts the low values higher, they move up more near the bright values. And 78% of the encoded values end up above the 127 50% midpoint (see LUT on next page, or see curve above). So to speak, the file data simply stores roughly the square root, and then the CRT decodes by showing it roughly squared, for no net change then, which was the plan, to reproduce the original linear data. The reason is because the CRT losses are going to show it squared regardless (but specifically, the CRT response result is power of 2.2).

Not to worry, our eye is NEVER EVER going to see any of these gamma values. Because, then the non-linear CRT gamma output is a roughly squared response to expand it back (restored to our first 225 and 25 linear values by the actual CRT losses that we planned for). CRT losses still greatly reduce the low values, but which were first boosted in preparation for it. So this gamma correction operation can properly show the dim values linearly again (since dim starts off condensed, up much closer to the strong values, and then becomes properly dim when expanded by CRT losses.) It has worked great for many years. But absolutely nothing about gamma is related to the human eye response. We don"t need to even care how the eye works. The eye NEVER sees any gamma data. The eye merely looks at the final linear reproduction of our image on the screen, after it is all over. The eye only wants to see an accurate linear reproduction of the original scene. How hard is that?

Then more recently, we invented LCD displays which became very popular. These were considered linear devices, so technically, they didn"t need CRT gamma anymore. But if we did create and use gamma-free devices, then our device couldn"t show any of the world"s gamma images properly, and the world could not show our images properly. And our gamma-free images would be incompatible with CRT too. There"s no advantage of that, so we"re locked into gamma, and for full compatibility, we simply just continue encoding our images with gamma like always before. This is easy to do today, it just means the LCD device simply includes a little chip to first decode gamma and then show the original linear result. Perhaps it is a slight wasted effort, but it"s easy, and reversible, and the compatibility reward is huge (because all the worlds images are gamma encoded). So no big deal, no problem, it works great. Again, the eye never sees any gamma data, it is necessarily decoded first back to the linear original. We may not even realize gamma is a factor in our images, but it always is. Our histograms do show the numerical gamma data values, but the eye never sees a gamma image. Never ever.

Printers and Macintosh: Our printers naturally expect to receive gamma images too (because that"s all that exists). Publishing and printer devices do also need some of gamma, not as much as 2.2 for the CRT, but the screening methods need most of it (for dot gain, which is when the ink soaks in to the paper and spreads wider). Until recently (2009), Apple Mac computers used gamma 1.8 images. They could use the same CRT monitors as Windows computers, and those monitors obviously were gamma 2.2, but Apple split this up. This 1.8 value was designed for the early laser printers that Apple manufactured then (and for publishing prepress), to be what the printer needed. Then the Mac video hardware added another 0.4 gamma correction for the CRT monitor, so the video result was an unspoken gamma 2.2, roughly — even if their files were gamma 1.8. That worked before internet, before images were shared widely. But now, the last few Mac versions (since OS 10.6) now observe the sRGB world standard gamma 2.2 in the file, because all the world"s images are already encoded that way, and we indiscriminately share them via the internet now. Compatibility is a huge deal, because all the worlds grayscale and color photo images are tonal images. All tonal images are gamma encoded. But yes, printers are also programmed to deal with the gamma 2.2 data they receive, and know to adjust it to their actual needs.

Extremely few PC computers could even show images before 1987. An early wide-spread source of images was Compuserve"s GIF file in 1987 (indexed color, an 8 bit index into a palette of 256 colors maximum, concerned with small file size and dialup modem speeds instead of image quality). Better for graphics, and indexed color is still good for most simple graphics (with not very many colors). GIF wasn"t great for color photos, but at the time, some of these did seem awesome seen on the CRT monitor. Then 8-bit JPG and TIF files (16.7 million possible colors) were developed a few years later, and 24-bit video cards (for 8-bit RGB color instead of indexed color) became the norm soon, and the internet came too, and in just a few years, use of breathtaking computer photos literally exploded to be seen everywhere. Our current 8 bits IS THE SOLUTION chosen to solve the problem, and it has been adequate for 30+ years. Specifically, the definitions are that these 8-bit files had three 8-bit RGB channels for 24 bit color, for RGB 256x256x256 = 16.7 million possible colors.

While we"re on history, this CRT problem (non-linear response curve named gamma) was solved by earliest television (first NTSC spec in 1941). Without this "gamma correction", the CRT screen images came out unacceptably dark. Television broadcast stations intentionally boosted the dark values (with gamma correction, encoded to be opposite to the expected CRT losses, that curve called gamma). That was vastly less expensive in vacuum tube days than building gamma circuitry into every TV set. Today, it"s just a very simple chip for the LCD monitors that don"t need gamma... LCD simply decodes it to remove gamma now, to restore it to linear.

This is certainly NOT saying gamma does not matter now. We still do gamma for compatibility (for CRT, and to see all of the worlds images, and so all the worlds systems can view our images). The LCD monitors simply know to decode and remove gamma 2.2, and for important compatibility, you do need to provide them with a proper gamma 2.2 to process, because 2.2 is what they will remove. sRGB profile is the standard way to do that. This is very easy, and mostly fully automatic, about impossible to bypass.

The 8-bit issue is NOT that 8-bit gamma data can only store integers in range of [0..255]. Meaning, we could use the same 8-bit gamma file for a 12 bit or 16 bit display device (if there were any). The only 8-bit issue is that our display devices can only show 8 bit data. See this math displayed on next page.

Unfortunately, some do like to imagine that gamma must still be needed (now for the eye?), merely because they once read Poynton that the low end steps in gamma data better matches the human eye 1% steps of perception. Possibly it may, but it was explained as coincidental. THIS COULD NOT MATTER LESS. They"re simply wrong about the need of the eye, it is false rationalization, obviously not realizing that our eye Never sees any gamma data. Never ever. We know to encode gamma correction of exponent 1/2.2 for CRT, which is needed because we"ve learned the lossy CRT response will do the opposite. It really wouldn"t matter which math operation we use for the linear LCD, if any, so long as the LCD still knows to do the exact opposite, to reverse it back out. But the LCD monitor necessarily does expect gamma 2.2 data anyway, and gamma 2.2 is exactly undone. Gamma data is universally present in existing images, and it is always first reversibly decoded back to be the original linear reproduction that our eye needs to view. That"s the goal, linear is exactly what our eye expects. Our eye never sees, and has no use for gamma data. It would be distortion if it ever did. But the CRT does have use for specific gamma data (to be able to show a linear reproduction that our eye wants).

Today, 8-bits is the sticky part: We do store computed gamma into 8-bit data and JPG files, which a LCD monitor does decode into their 8-bit video space (I would make sure any lower cost LCD actually has specifications saying "16.7 million colors", which means 8-bits. In the past, some were just 6 bits, which is 0.262 million colors, not a bragging point to advertise). I"d suggest that serious photo users search their dealer for an "IPS monitor" that specifies 16.7 million colors (just meaning 8 bits). Price of many 23 inch IPS models is down around $150 US now.

How big a deal is gamma in 8-bits? We hear theories, but we all use 8-bit video, and we seem pretty happy with how it works, because it"s very adequate (it might be a best compromise for cost, but if it were not adequate, we would have done it another way by now). But our cameras and scanners are not 8-bit devices. We can use 8 bit gamma files for 12 or 16 bit images (and our cameras and scanners do that), and also for 12 and 16 bit display devices (if any, if with proper drivers). We tend to blame any imagined problem on 8 bit gamma, but the only actual issue is with 8 bit display devices. There is a closer look at this math situation on the next page.

In 12 bits, as if it were a choice in gamma (it"s not a choice so far), there are 4096 possible values (finer steps, closer choices). In 8 bits, there are 256 possible values, from 0 to 255. From linear 80, the calculated gamma value 150.56 must become integer 150 or 151. If rounded to 151, it would decode back to 80.52, which has to be called 81, which is not 80 (an Off by One error). We can round it or truncate it. If we round it, we throw some values off. If we don"t, we throw other values off. It"s not predictable after we do the exponentiation. The system has no clue which way would be best for any specific sample. More precision could help, but it is quite minor, and questionable if worth the cost. Actually, for that, it would seem best to not use gamma at all, and simply just store 80 linear in the file, and then directly read it as 80, with no question about how to reproduce linear. But that does not solve the CRT problem, which is why we use gamma.

So that"s some of the stuff we hear about gamma. It"s just normal rounding, little stuff. We can"t even perceive vision differences of less than about 1%. Which to see generally requires a change of 1 at RGB(100) or 2 at RGB(200), which is a stretch for these gamma issues. Humans have thresholds before we can detect changes in things like vision, etc. (start at Wikipedia: Weber Fechner Law, and on to Just Noticeable Difference).

Our cameras and scanners are typically 12 bits today, which is about improving dynamic range. 12 bits has more dynamic range than 8 bits (it captures more detail into darker blacks). Sure, we"re still going to convert it to 8 bits for our monitors and printers, but there"s still a difference. The camera captures a 12 bit image, and the gamma operation normalizes all of the data into a 0..1 range. Our new 8-bit data does not just chop it off at 8-bits, but instead gamma scales this 0..1 range proportionately into 8 bits, a percentage between 0..1, but fitting into a smaller space (of 0..255 values). Saying, if the dark tone were at 1% of 4095 12-bits, it will also be at 1% of 255 8-bits. That might be low data values of 2 or 3, but it is theoretically there. This might be what Poynton is getting at (still requiring gamma), but I think he doesn"t say it. So our image does still contain hints of the 12-bit detail, more or less (it is 8-bit data) However yes, it is compressed into the range of 8-bits, and NOT just chopped off at 8-bits. It"s still there. That"s a difference.

The obvious purpose of gamma was to necessarily support CRT monitors, and now that LCD monitors have replaced CRT, we could use an 8-bit camera that outputs 8-bit linear directly, and our LCD monitor could just show the linear image directly, bypassing its operation to decode and discard gamma. And that could work (on that one equipped LCD), but it would just chop off range at 8-bits. Unless the camera were higher bit count and also did this proportional 0..1 scaling, which gamma just happens to already do. And continuing gamma is simple to do, which also does not obsolete all of the worlds old images and old viewing devices. That"s my take.

Truncation was popular for gamma in the earlier days, it is very simple and very fast, and was all the simplest CPU chips could do then. Affects different values, but worse results. However today, we have the LookUp table chips (LUT, next page), and they are easily created with rounded data. If we use the rounded value, most of the values work out very well, but other possible values might still be off by one. Off by one going to happen, but it"s a minor problem, all at the high end where it really doesn"t matter. Sometimes the numbers can look kinda bad, until we realize it"s only Off by One. But for example, if rounded, maybe 28% of the integer values are still simply not exactly reproducible (encoded and then decoded back to same linear number, off by one). In rounded 8-bits, some of these will be Off by One (it is the least possible error). But if rounded, only five of the 256 values will barely reach 1%, which is arguably enough for those few values to perhaps be slightly just detectable to the eye (it"s very optimistic that we might ever notice it down among all of the pixels).

Note that Options 6 & 7 normalize the data to a [0..1] range, then convert linear values to gamma, and then back to linear, and looks for a difference due to 8-bit rounding. Option 6 does any one value, but Option 7 does all possible values, to see how things are going. But our photos were all encoded elsewhere at 12 bits (in the camera, or in the scanner, or in raw, etc), so encoding is not our 8-bit issue (it"s already done). So my procedure is that Option 6 & 7 always round the Input encoded values, and only uses the Truncate gamma values checkbox for the decoding, which will convert the 8-bit output values by either truncating or by full rounding. This still presents 8-bit integer values to be decoded, which matches the real world, but rounding the input introduces less error, which the camera likely would not cause.

Our 8-bit video does seem adequate. One possible exception might be a large gradient filling most of the screen width (needing more values to not show noticeable differences, i.e., banding), but that is not a photo situation. Hollywood graphics might see it. In general, our monitors black level cannot show differences in the lowest black tones. And our human eyes cannot detect less than 1% differences at the high end.

These cookies help to improve the performance of BenQ. If you want to opt-out of advertising cookies, you have to turn-off performance cookies. We also use Google Analytics, SessionCam and Hotjar to track activity and performance on the BenQ website. You can control the information provided to Google, SessionCam and Hotjar.  To opt out of certain ads provided by Google you can use any of the methods set forth here or using the Google Analytics opt out browser add-on here. To opt-out of SessionCam collecting data, you can disable tracking completely by following link：https://www.hotjar.com/privacy/do-not-track/.

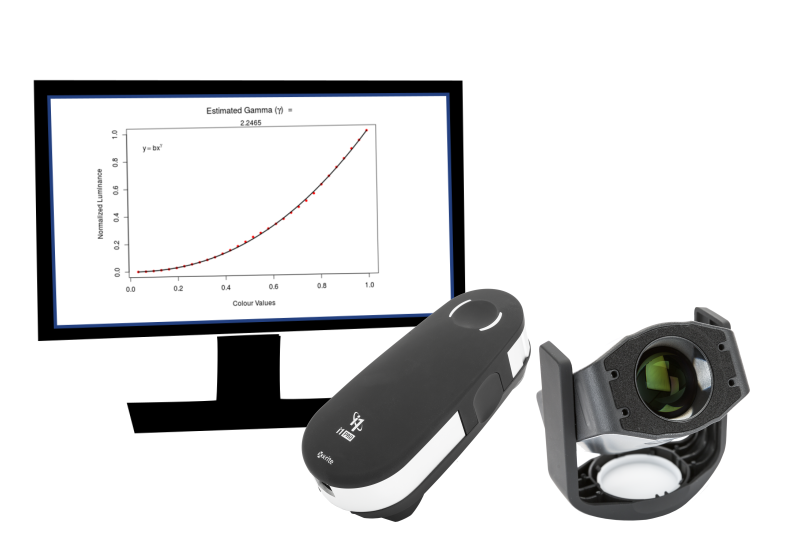
With most display systems, the gamma correction is applied in the video card (by downloading a custom LUT into the card). Some of the higher-end monitors (high end NEC & Eizo monitors) have the ability to apply a correction LUT internally inside the monitor. The advantage of this is that they are generally higher bit depth (typically 10 or 12 bits) than the correction applied via the display card (8-bits).

As it seems from FreddyNZ"s calibration image my LCD monitor is totally "screwed up".As freddyNZ mentioned, the correction LUT isn"t automatically calculated, as it depends upon the individual characteristics of the display (CRT or LCD) being used. If you"re using a hardware display calibrator, it starts off by loading a linear LUT into the video card and then proceeds to measure the characteristics of the display. It then calulates a correction LUT that will bring the display to a known gamma & color temperature and loads that into the video card (or monitor if supported). After calibrating the display to known set of values, it then proceeds to characterize the color characteristics of the display. This data is used to build the ICC profile for the display. Note that if you use a display that doesn"t support an internal correction LUT (that"s most of us), the correction LUT gets loaded into the video card when the OS boots up. It is usually done with a small LUT loader utility which runs at startup and reads the correction LUT from the default display profile and loads it into the video card.

Do you happen to know if a correction LUT made by a hardware calibrator is stored inside the ICC profile you mention? Or are the monitor"s ICC profile and the correction LUT two totally different things?

"When the data is saved, after being gamma corrected to 1.8, that gamma correction stays with the file. However, most file formats (GIF, JPEG) don"t have anyway to tell a user the gamma correction that has already been applied to image data. Therefore, the user must guess and gamma correct until he is satisfied with how it looks. The Targa and PNG file formats do encode the exact gamma information, removing some of the guess work. The 3D modeling program, 3D Studio, actually takes advantage of this information!

Gamma correction, then, can be done on file data directly (the individual bits in the file are changed to reflect the correction). This is what is meant by the File Gamma or "gamma of a file." On the other hand gamma correction can be done as post processing on file data. In the latter case, the data in the file is unchanged, but between reading the file and displaying the data on your monitor, the data is gamma corrected for display purposes. Ideally, if one knows the File Gamma and their own System Gamma, they can determine the gamma correction needed (if any) to accurately display the file on their system."

So are gamma corrected values stored often in image files by image editing software? And do any programs really take it into consideration when showing this kind of image file by lowering midtones of the image before sending it to video card? So is this "file gamma" really a common problem among photo editing or a very rare exception?

This is the second installment of a 2-part guest post by Jim Perkins, a professor at the Rochester Institute of Technology"s medical illustration program. His first post detailed why it"s a good idea to calibrate your computer monitor regularly. This next post walks us through the process and explains the mysterious settings known as gamma and white point.

If you have never calibrated your monitor, it’s almost certainly out of whack. Maybe a lot. Maybe a little. There’s really no way to know unless you generate an expensive prepress proof (e.g., a Kodak Approval, Fuji FinalProof, Creo Veris) and compare it to the on-screen image. Even a high quality monitor may not display colors accurately, especially as it ages. All monitors change over time, so calibration must be done on a regular basis. Most experts recommend doing it every few weeks to every few months.

In practice, however, calibration is a little bit trickier. First of all, you need to control some aspects of the monitor’s environment to ensure proper calibration. Second, you must make some critical decisions about how you want the monitor to display color. As I’ll discuss below, these decisions depends on whether you are creating art primarily for print, on-screen display (web, gaming), or broadcast (TV/film).

Calibration should be done under the same conditions that you normally use the monitor. You don’t want to calibrate under one set of conditions and use the monitor under different conditions. It won’t look the same. For example, a monitor’s display can change as it warms up. So be sure to turn the monitor on at least 30 minutes before calibrating so it warms up to normal operating temperature. This was more of a concern with old CRT monitors, but applies to flat panel LCDs as well.

Next, make sure you are using your monitor under moderate ambient lighting conditions. It’s not necessary to work in the dark, but the monitor should be the strongest light source in your work area. Don’t have strong lights shining directly on the screen, as this will affect the apparent brightness of the display and can introduce a color cast. Some calibration systems have ambient light sensors to compensate for this, but they’re not perfect.

Some photo studios and prepress services go so far as to paint their walls and furniture a neutral 50% gray and use only daylight-balanced D50 fluorescent lights. The International Organization for Standardization (ISO – www.iso.org) publishes a set of guidelines called “Graphic Technology and Photography -- Viewing Conditions” (ISO 3664:2009) for photographers, artists, and web developers; and a stricter set of guidelines for photo imaging labs and prepress service bureaus called “Graphic Technology - Displays for Colour Proofing - Characteristics and Viewing Conditions” (ISO 12646:2008). This is probably overkill for most artists.

When you connect the colorimeter and run the calibration software, it will ask you to select some important settings. The two most important settings are gamma and color temperature, both of which are fairly difficult concepts to understand.

Gamma is the relationship between the numerical value of a pixel in an image file and the brightness of that pixel when viewed on screen. The computer translates the numerical values in the image file into voltage that is sent to the monitor. This relationship is non-linear, meaning that a change in voltage does not translate into an equivalent change in brightness. For almost all TVs and computer monitors, a change in voltage results in a change in brightness raised to the 2.5 power. The gamma for these devices, therefore, is said to be 2.5.

Gamma correction is a way of compensating for this non-linear relationship between voltage and brightness. A combination of hardware and/or software can reduce the gamma to something closer to 1.0, i.e. a perfect linear relationship. This helps ensure that a change in pixel value in the digital file translates into a proportional change in brightness on screen.

Prior to calibrating a monitor, it is critical to tell the calibration software which gamma setting you wish to use. Historically, there has been a big difference in hardware gamma correction between Macs and PCs. For many years, this dictated the choice of gamma on these two platforms. However, as we’ll see below, the choice now depends more on the type of work you do and not on the operating system.

Since its introduction in 1984, the Macintosh computer had built-in correction that brought the gamma of the system down to 1.8. Therefore, we say that the “system gamma” of Macs is 1.8. Apple chose this number for a very good reason. It turns out that printing devices have a type of gamma also. A 10% gray area of pixels in a digital file is printed as a series of tiny dots that cover 10% of the surface of the paper. In theory, this should produce the appearance of a 10% gray on paper, matching the value in the digital file. In practice, however, the ink or toner bleeds into the paper and spreads (called “dot gain”), creating a pattern of dots that covers more than 10% of the paper. This makes the printed image appear darker than it should, especially in the midtones. The Mac system gamma of 1.8 compensates for this phenomenon, making the image slightly lighter so it matches the digital file.

The original Mac was designed from the outset to be a graphic arts system. Its release coincided with the introduction of the Apple Laserwriter, the Linotype Linotronics imagesetter, and Aldus Pagemaker, the first page layout program. All of these components were tied together by the PostScript page description language, also released in 1984 by a fledgling company called Adobe. This launched the desktop publishing revolution of the mid-1980s and beyond. It was no coincidence that Apple chose a system gamma that was geared towards print output.

Windows PCs, on the other hand, have never had built-in gamma correction, although this is an option on some graphics cards. This reflects the fact that PCs were always targeted towards business and the mass consumer market rather than to graphics professionals. With no hardware correction, the Windows system gamma is about 2.2.

With the release of Mac OSX 10.6 (Snow Leopard) in 2009, Apple finally changed their default system gamma from 1.8 to 2.2. They did this, of course, to ensure that video games and web images looked the same on Mac and PC systems. In doing so, however, they abandoned their traditional base of support among graphics professionals.

The choice of gamma settings, therefore, is no longer dictated by the computer platform or operating system. Instead, when calibrating your monitor, you can choose a gamma setting that is best suited to the type of work you normally do. This will override the built-in settings of the system.

If you create mostly images that will be viewed on screen – for the web, PowerPoint, video games, etc. – set your gamma to 2.2. This will help ensure that your images look consistent across the widest range of computers used in business and the mass consumer market.

On the other hand, if you still create most of your work for print (as I do), stick with 1.8. Not only is this setting more compatible with high-end printing system, it also produces noticeably lighter images on screen. This helps you see detail in shadows, something that is critical when creating and editing digital images.

Physicists express the temperature of the ideal black body in degrees Kelvin (°K). This is just a different scale for measuring temperature, like Celsius and Fahrenheit. The Kelvin scale is noteworthy because zero degrees on the Kelvin scale is known as Absolute Zero – the temperature at which all molecular motion stops (equal to -459.67° on the Fahrenheit scale)

So what does this have to do with monitor calibration? There is no such thing as pure white. Every light source has a slight hue or color cast to it. For any given light source, we can match it up to a temperature on the Kelvin scale that emits the same color of light. Below is a list of lighting conditions and their corresponding color temperatures:

Any white objects that appear on your computer screen will have one of these color casts. You probably don’t notice it because you are accustomed to thinking of a blank page on screen as being “pure” white. However, if you change the color temperature of your monitor, you will see a dramatic difference and the color cast will become obvious. On the Mac, go to the Monitor controls under System Preferences. Select the Color tab and click Calibrate. Here you have the option of changing both the gamma setting and color temperature to see how they affect your screen. However, I recommend you DO NOT save any of thes