gamma correction for lcd monitors pricelist

Problems like extremely poor display of shadow areas, blown-out highlights, or images prepared on Macs appearing too dark on Windows computers are often due to gamma characteristics. In this session, we"ll discuss gamma, which has a significant impact on color reproduction on LCD monitors. Understanding gamma is useful in both color management and product selection. Users who value picture quality are advised to check this information.

* Below is the translation from the Japanese of the ITmedia article "Is the Beauty of a Curve Decisive for Color Reproduction? Learning About LCD Monitor Gamma" published July 13, 2009. Copyright 2011 ITmedia Inc. All Rights Reserved.

The term gamma comes from the third letter of the Greek alphabet, written Γ in upper case and γ in lower case. The word gamma occurs often in everyday life, in terms like gamma rays, the star called Gamma Velorum, and gamma-GTP. In computer image processing, the term generally refers to the brightness of intermediate tones (gray).

Let"s discuss gamma in a little more detail. In a PC environment, the hardware used when working with color includes monitors, printers, and scanners. When using these devices connected to a PC, we input and output color information to and from each device. Since each device has its own unique color handling characteristics (or tendencies), color information cannot be output exactly as input. The color handling characteristics that arise in input and output are known as gamma characteristics.

While certain monitors are also compatible with color handling at 10 bits per RGB color (210 = 1024 tones), or 1024 x 3 (approximately 1,064,330,000 colors), operating system and application support for such monitors has lagged. Currently, some 16.77 million colors, with eight bits per RGB color, is the standard color environment for PC monitors.

When a PC and a monitor exchange color information, the ideal is a relationship in which the eight-bit color information per RGB color input from the PC to the monitor can be output accurately—that is, a 1:1 relationship for input:output. However, since gamma characteristics differ between PCs and monitors, color information is not transmitted according to a 1:1 input:output relationship.

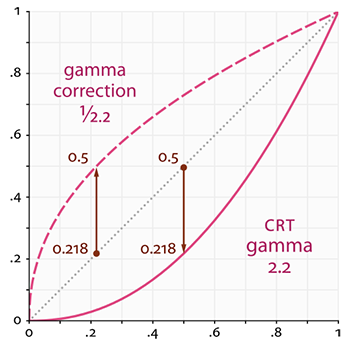
How colors ultimately look depends on the relationship resulting from the gamma values (γ) that numerically represent the gamma characteristics of each hardware device. If the color information input is represented as x and output as y, the relationship applying the gamma value can be represented by the equation y = xγ.

Gamma characteristics are represented by the equation y = xγ. At the ideal gamma value of 1.0, y = x; but since each monitor has its own unique gamma characteristics (gamma values), y generally doesn"t equal x. The above graph depicts a curve adjusted to the standard Windows gamma value of 2.2. The standard gamma value for the Mac OS is 1.8.

Ordinarily, the nature of monitor gamma is such that intermediate tones tend to appear dark. Efforts seek to promote accurate exchange of color information by inputting data signals in which the intermediate tones have already been brightened to approach an input:output balance of 1:1. Balancing color information to match device gamma characteristics in this way is called gamma correction.

A simple gamma correction system. If we account for monitor gamma characteristics and input color information with gamma values adjusted accordingly (i.e., color information with intermediate tones brightened), color handling approaches the y = x ideal. Since gamma correction generally occurs automatically, users usually obtain correct color handling on a PC monitor without much effort. However, the precision of gamma correction varies from manufacturer to manufacturer and from product to product (see below for details).

In most cases, if a computer runs the Windows operating system, we can achieve close to ideal colors by using a monitor with a gamma value of 2.2. This is because Windows assumes a monitor with a gamma value of 2.2, the standard gamma value for Windows. Most LCD monitors are designed based on a gamma value of 2.2.

The standard monitor gamma value for the Mac OS is 1.8. The same concept applies as in Windows. We can obtain color reproduction approaching the ideal by connecting a Mac to a monitor configured with a gamma value of 1.8.

An example of the same image displayed at gamma values of 2.2 (photo at left) and 1.8 (photo at right). At a gamma value of 1.8, the overall image appears brighter. The LCD monitor used is EIZO"s 20-inch wide-screen EV2023W FlexScan model (ITmedia site).

To equalize color handling in mixed Windows and Mac environments, it"s a good idea to standardize the gamma values between the two operating systems. Changing the gamma value for the Mac OS is easy; but Windows provides no such standard feature. Since Windows users perform color adjustments through the graphics card driver or separate color-adjustment software, changing the gamma value can be an unexpectedly complex task. If the monitor used in a Windows environment offers a feature for adjusting gamma values, obtaining more accurate results will likely be easier.

If we know that a certain image was created in a Mac OS environment with a gamma value of 1.8, or if an image received from a Mac user appears unnaturally dark, changing the monitor gamma setting to 1.8 should show the image with the colors intended by the creator.

Eizo Nanao"s LCD monitors allow users to configure the gamma value from the OSD menu, making this procedure easy. In addition to the initially configured gamma value of 2.2., one can choose from multiple settings, including the Mac OS standard of 1.8.

To digress slightly, standard gamma values differ between Windows and Mac OS for reasons related to the design concepts and histories of the two operating systems. Windows adopted a gamma value corresponding to television (2.2), while the Mac OS adopted a gamma value corresponding to commercial printers (1.8). The Mac OS has a long history of association with commercial printing and desktop publishing applications, for which 1.8 remains the basic gamma value, even now. On the other hand, a gamma value of 2.2 is standard in the sRGB color space, the standard for the Internet and for digital content generally, and for Adobe RGB, the use of which has expanded for wide-gamut printing,.

Given the proliferating use of color spaces like sRGB and Adobe RGB, plans call for the latest Mac OS scheduled for release by Apple Computer in September 2009, Mac OS X 10.6 Snow Leopard, to switch from a default gamma value of 1.8 to 2.2. A gamma value of 2.2 is expected to become the future mainstream for Macs.

On the preceding page, we mentioned that the standard gamma value in a Windows environment is 2.2 and that many LCD monitors can be adjusted to a gamma value of 2.2. However, due to the individual tendencies of LCD monitors (or the LCD panels installed in them), it"s hard to graph a smooth gamma curve of 2.2.

Traditionally, LCD panels have featured S-shaped gamma curves, with ups and downs here and there and curves that diverge by RGB color. This phenomenon is particularly marked for dark and light tones, often appearing to the eye of the user as tone jumps, color deviations, and color breakdown.

The internal gamma correction feature incorporated into LCD monitors that emphasize picture quality allows such irregularity in the gamma curve to be corrected to approach the ideal of y = x γ. Device specs provide one especially useful figure to help us determine whether a monitor has an internal gamma correction feature: A monitor can be considered compatible with internal gamma correction if the figure for maximum number of colors is approximately 1,064,330,000 or 68 billion or if the specs indicate the look-up table (LUT) is 10- or 12-bit.

An internal gamma correction feature applies multi-gradation to colors and reallocates them. While the input from a PC to an LCD monitor is in the form of color information at eight bits per RGB color, within the LCD monitor, multi-gradation is applied to increase this to 10 bits (approximately 1,064,330,000 colors) or 12 bits (approximately 68 billion colors). The optimal color at eight bits per RGB color (approximately 16.77 million colors) is identified by referring to the LUT and displayed on screen. This corrects irregularity in the gamma curve and deviations in each RGB color, causing the output on screen to approach the ideal of y = x γ.

Let"s look at a little more information on the LUT. The LUT is a table containing the results of certain calculations performed in advance. The results for certain calculations can be obtained simply by referring to the LUT, without actually performing the calculations. This accelerates processing and reduces the load on a system. The LUT in an LCD monitor identifies the optimal eight-bit RGB colors from multi-gradation color data of 10 or more bits.

An overview of an internal gamma correction feature. Eight-bit RGB color information input from the PC is subjected to multi-gradation to 10 or more bits. This is then remapped to the optimal eight-bit RGB tone by referring to the LUT. Following internal gamma correction, the results approach the ideal gamma curve, dramatically improving on screen gradation and color reproduction.

Eizo Nanao"s LCD monitors proactively employ internal gamma correction features. In models designed especially for high picture quality and in some models in the ColorEdge series designed for color management, eight-bit RGB input signals from the PC are subjected to multi-gradation, and calculations are performed at 14 or 16 bits. A key reason for performing calculations at bit counts higher than the LUT bit count is to improve gradation still further, particularly the reproduction of darker tones. Users seeking high-quality color reproduction should probably choose a monitor model like this one.

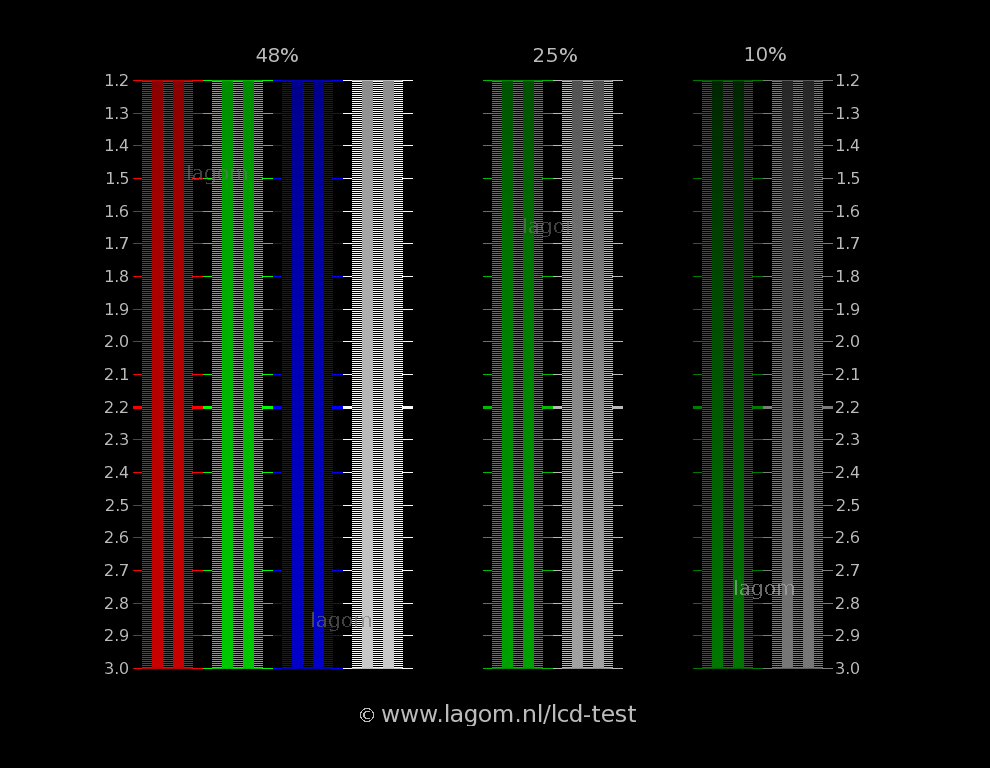
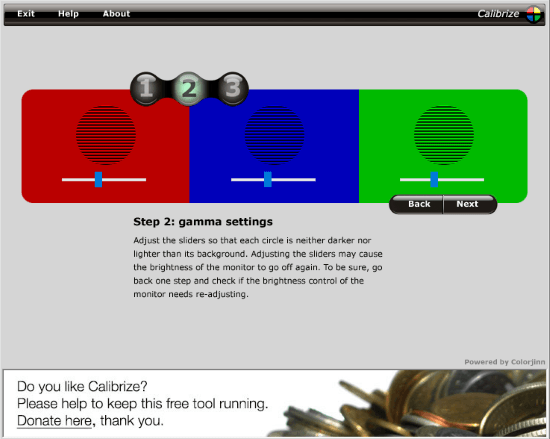
In conclusion, we"ve prepared image patterns that make it easy to check the gamma values of an LCD monitor, based on this session"s discussion. Looking directly at your LCD monitor, move back slightly from the screen and gaze at the following images with your eyes half-closed. Visually compare the square outlines and the stripes around them, looking for patterns that appear to have the same tone of gray (brightness). The pattern for which the square frame and the striped pattern around it appear closest in brightness represents the rough gamma value to which the monitor is currently configured.

Based on a gamma value of 2.2, if the square frame appears dark, the LCD monitor"s gamma value is low. If the square frame appears bright, the gamma value is high. You can adjust the gamma value by changing the LCD monitor"s brightness settings or by adjusting brightness in the driver menu for the graphics card.

Naturally, it"s even easier to adjust the gamma if you use a model designed for gamma value adjustments, like an EIZO LCD monitor. For even better color reproduction, you can set the gamma value and optimize color reproduction by calibrating your monitor.

With the SVX-4096 LCD controller board you can have your own gamma correction curve lookup tables together with custom on-screen menu entries to select them.

Being able to calibrate a display system is essential for some applications such as viewing medical images on a DICOM compliant monitor. On the SVX-4096 you can provide us (Digital View) with the look-up table data and we will create a custom labeled on-screen menu entry or RS-232 command to call up those settings. Alternatively we can calibrate your chosen panel kit as an engineering service.

Software, Controller Utility: It is worth having a look at the Controller Utility application that provides a user interface for modification of the gamma curve. See the Software section here. It is a free download for Microsoft  Windows providing access to a lot of controller functions in addition to the gamma curve adjustment.

DICOM note: DICOM (Digital Imaging and Communications in Medicine) is a standard covering the distribution and viewing of medical images. The SVX-4096 DICOM support takes the form of calibration using a color analyzer to build a gamma curve LUT (Lookup Table) for a specified LCD panel and then code this into the firmware of the SVX-4096.

The DICOM LUT is then available as a setting within the OSD commands of the controller. The important point is that this is LCD panel model specific though the good news is that many LCD panels these days meet the criteria for calibration.

Calibrating your monitor manually is very straightforward. And almost all of us will need to do this at one point or another. For the majority of us a manual calibration will do just fine. This approach uses your computer’s pre-built calibration software to enhance and adjust your monitor’s color balance.

The first step involves some basic prep. Look out for the signs that your monitor needs calibration and, if in doubt, do it anyway! Calibration is especially important for high-resolution monitors if you want to benefit fully from the full breadth of color on offer.

It’s important that your monitor is out of direct sunlight during the calibration process Aim for neutral lighting away from any artificial or direct natural light.

Connect your monitor to a laptop or computer using either a display port or HDMI cable. Then leave your monitor to warm up for approximately 30 minutes, ensuring that it doesn’t go into hibernation mode – you may need to stay nearby to jiggle the mouse around and prevent the screen from turning off.

Before commencing calibration, turn your monitor’s resolution back to its default settings. To do this on Windows PC simply navigate to Settings > System > Display > Resolution > Recommended. To do this on Mac navigate to System preferences > Displays > Display tab > default for display.

This website is using a security service to protect itself from online attacks. The action you just performed triggered the security solution. There are several actions that could trigger this block including submitting a certain word or phrase, a SQL command or malformed data.

Gamma is an important but seldom understood characteristic of virtually all digital imaging systems. It defines the relationship between a pixel"s numerical value and its actual luminance. Without gamma, shades captured by digital cameras wouldn"t appear as they did to our eyes (on a standard monitor). It"s also referred to as gamma correction, gamma encoding or gamma compression, but these all refer to a similar concept. Understanding how gamma works can improve one"s exposure technique, in addition to helping one make the most of image editing.

1. Our eyes do not perceive light the way cameras do. With a digital camera, when twice the number of photons hit the sensor, it receives twice the signal (a "linear" relationship). Pretty logical, right? That"s not how our eyes work. Instead, we perceive twice the light as being only a fraction brighter — and increasingly so for higher light intensities (a "nonlinear" relationship).

Compared to a camera, we are much more sensitive to changes in dark tones than we are to similar changes in bright tones. There"s a biological reason for this peculiarity: it enables our vision to operate over a broader range of luminance. Otherwise the typical range in brightness we encounter outdoors would be too overwhelming.

But how does all of this relate to gamma? In this case, gamma is what translates between our eye"s light sensitivity and that of the camera. When a digital image is saved, it"s therefore "gamma encoded" — so that twice the value in a file more closely corresponds to what we would perceive as being twice as bright.

Technical Note: Gamma is defined by Vout = Vingamma , where Vout is the output luminance value and Vin is the input/actual luminance value. This formula causes the blue line above to curve. When gamma<1, the line arches upward, whereas the opposite occurs with gamma>1.

2. Gamma encoded images store tones more efficiently. Since gamma encoding redistributes tonal levels closer to how our eyes perceive them, fewer bits are needed to describe a given tonal range. Otherwise, an excess of bits would be devoted to describe the brighter tones (where the camera is relatively more sensitive), and a shortage of bits would be left to describe the darker tones (where the camera is relatively less sensitive):

Notice how the linear encoding uses insufficient levels to describe the dark tones — even though this leads to an excess of levels to describe the bright tones. On the other hand, the gamma encoded gradient distributes the tones roughly evenly across the entire range ("perceptually uniform"). This also ensures that subsequent image editing, color and histograms are all based on natural, perceptually uniform tones.

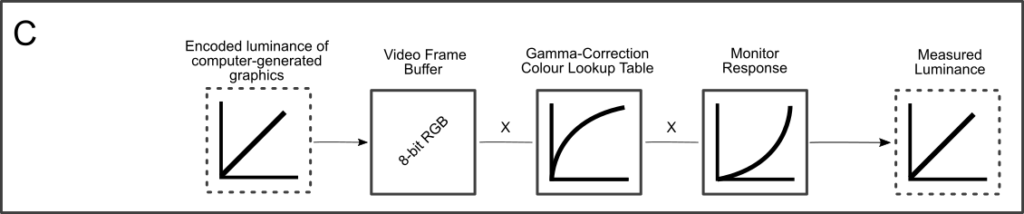
Despite all of these benefits, gamma encoding adds a layer of complexity to the whole process of recording and displaying images. The next step is where most people get confused, so take this part slowly. A gamma encoded image has to have "gamma correction" applied when it is viewed — which effectively converts it back into light from the original scene. In other words, the purpose of gamma encoding is for recording the image — not for displaying the image. Fortunately this second step (the "display gamma") is automatically performed by your monitor and video card. The following diagram illustrates how all of this fits together:

1. Image Gamma. This is applied either by your camera or RAW development software whenever a captured image is converted into a standard JPEG or TIFF file. It redistributes native camera tonal levels into ones which are more perceptually uniform, thereby making the most efficient use of a given bit depth.

2. Display Gamma. This refers to the net influence of your video card and display device, so it may in fact be comprised of several gammas. The main purpose of the display gamma is to compensate for a file"s gamma — thereby ensuring that the image isn"t unrealistically brightened when displayed on your screen. A higher display gamma results in a darker image with greater contrast.

3. System Gamma. This represents the net effect of all gamma values that have been applied to an image, and is also referred to as the "viewing gamma." For faithful reproduction of a scene, this should ideally be close to a straight line (gamma = 1.0). A straight line ensures that the input (the original scene) is the same as the output (the light displayed on your screen or in a print). However, the system gamma is sometimes set slightly greater than 1.0 in order to improve contrast. This can help compensate for limitations due to the dynamic range of a display device, or due to non-ideal viewing conditions and image flare.

The precise image gamma is usually specified by a color profile that is embedded within the file. Most image files use an encoding gamma of 1/2.2 (such as those using sRGB and Adobe RGB 1998 color), but the big exception is with RAW files, which use a linear gamma. However, RAW image viewers typically show these presuming a standard encoding gamma of 1/2.2, since they would otherwise appear too dark:

If no color profile is embedded, then a standard gamma of 1/2.2 is usually assumed. Files without an embedded color profile typically include many PNG and GIF files, in addition to some JPEG images that were created using a "save for the web" setting.

Technical Note on Camera Gamma. Most digital cameras record light linearly, so their gamma is assumed to be 1.0, but near the extreme shadows and highlights this may not hold true. In that case, the file gamma may represent a combination of the encoding gamma and the camera"s gamma. However, the camera"s gamma is usually negligible by comparison. Camera manufacturers might also apply subtle tonal curves, which can also impact a file"s gamma.

This is the gamma that you are controlling when you perform monitor calibration and adjust your contrast setting. Fortunately, the industry has converged on a standard display gamma of 2.2, so one doesn"t need to worry about the pros/cons of different values. Older macintosh computers used a display gamma of 1.8, which made non-mac images appear brighter relative to a typical PC, but this is no longer the case.

Recall that the display gamma compensates for the image file"s gamma, and that the net result of this compensation is the system/overall gamma. For a standard gamma encoded image file (—), changing the display gamma (—) will therefore have the following overall impact (—) on an image:

Recall from before that the image file gamma (—) plus the display gamma (—) equals the overall system gamma (—). Also note how higher gamma values cause the red curve to bend downward.

If you"re having trouble following the above charts, don"t despair! It"s a good idea to first have an understanding of how tonal curves impact image brightness and contrast. Otherwise you can just look at the portrait images for a qualitative understanding.

How to interpret the charts. The first picture (far left) gets brightened substantially because the image gamma (—) is uncorrected by the display gamma (—), resulting in an overall system gamma (—) that curves upward. In the second picture, the display gamma doesn"t fully correct for the image file gamma, resulting in an overall system gamma that still curves upward a little (and therefore still brightens the image slightly). In the third picture, the display gamma exactly corrects the image gamma, resulting in an overall linear system gamma. Finally, in the fourth picture the display gamma over-compensates for the image gamma, resulting in an overall system gamma that curves downward (thereby darkening the image).

The overall display gamma is actually comprised of (i) the native monitor/LCD gamma and (ii) any gamma corrections applied within the display itself or by the video card. However, the effect of each is highly dependent on the type of display device.

CRT Monitors. Due to an odd bit of engineering luck, the native gamma of a CRT is 2.5 — almost the inverse of our eyes. Values from a gamma-encoded file could therefore be sent straight to the screen and they would automatically be corrected and appear nearly OK. However, a small gamma correction of ~1/1.1 needs to be applied to achieve an overall display gamma of 2.2. This is usually already set by the manufacturer"s default settings, but can also be set during monitor calibration.

LCD Monitors. LCD monitors weren"t so fortunate; ensuring an overall display gamma of 2.2 often requires substantial corrections, and they are also much less consistent than CRT"s. LCDs therefore require something called a look-up table (LUT) in order to ensure that input values are depicted using the intended display gamma (amongst other things). See the tutorial on monitor calibration: look-up tables for more on this topic.

Technical Note: The display gamma can be a little confusing because this term is often used interchangeably with gamma correction, since it corrects for the file gamma. However, the values given for each are not always equivalent. Gamma correction is sometimes specified in terms of the encoding gamma that it aims to compensate for — not the actual gamma that is applied. For example, the actual gamma applied with a "gamma correction of 1.5" is often equal to 1/1.5, since a gamma of 1/1.5 cancels a gamma of 1.5 (1.5 * 1/1.5 = 1.0). A higher gamma correction value might therefore brighten the image (the opposite of a higher display gamma).

Dynamic Range. In addition to ensuring the efficient use of image data, gamma encoding also actually increases the recordable dynamic range for a given bit depth. Gamma can sometimes also help a display/printer manage its limited dynamic range (compared to the original scene) by improving image contrast.

Gamma Correction. The term "gamma correction" is really just a catch-all phrase for when gamma is applied to offset some other earlier gamma. One should therefore probably avoid using this term if the specific gamma type can be referred to instead.

Gamma Compression & Expansion. These terms refer to situations where the gamma being applied is less than or greater than one, respectively. A file gamma could therefore be considered gamma compression, whereas a display gamma could be considered gamma expansion.

Applicability. Strictly speaking, gamma refers to a tonal curve which follows a simple power law (where Vout = Vingamma), but it"s often used to describe other tonal curves. For example, the sRGB color space is actually linear at very low luminosity, but then follows a curve at higher luminosity values. Neither the curve nor the linear region follow a standard gamma power law, but the overall gamma is approximated as 2.2.

Is Gamma Required? No, linear gamma (RAW) images would still appear as our eyes saw them — but only if these images were shown on a linear gamma display. However, this would negate gamma"s ability to efficiently record tonal levels.

The effect of gamma correction on an image: The original image was taken to varying powers, showing that powers larger than 1 make the shadows darker, while powers smaller than 1 make dark regions lighter.

Gamma correction or gamma is a nonlinear operation used to encode and decode luminance or tristimulus values in video or still image systems.power-law expression:

Gamma encoding of images is used to optimize the usage of bits when encoding an image, or bandwidth used to transport an image, by taking advantage of the non-linear manner in which humans perceive light and color.lightness), under common illumination conditions (neither pitch black nor blindingly bright), follows an approximate power function (which has no relation to the gamma function), with greater sensitivity to relative differences between darker tones than between lighter tones, consistent with the Stevens power law for brightness perception. If images are not gamma-encoded, they allocate too many bits or too much bandwidth to highlights that humans cannot differentiate, and too few bits or too little bandwidth to shadow values that humans are sensitive to and would require more bits/bandwidth to maintain the same visual quality.floating-point images is not required (and may be counterproductive), because the floating-point format already provides a piecewise linear approximation of a logarithmic curve.

Although gamma encoding was developed originally to compensate for the input–output characteristic of cathode ray tube (CRT) displays, it is not its main purpose or advantage in modern systems. In CRT displays, the light intensity varies nonlinearly with the electron-gun voltage. Altering the input signal by gamma compression can cancel this nonlinearity, such that the output picture has the intended luminance. However, the gamma characteristics of the display device do not play a factor in the gamma encoding of images and video. They need gamma encoding to maximize the visual quality of the signal, regardless of the gamma characteristics of the display device.

Analogously, digital cameras record light using electronic sensors that usually respond linearly. In the process of rendering linear raw data to conventional RGB data (e.g. for storage into JPEG image format), color space transformations and rendering transformations will be performed. In particular, almost all standard RGB color spaces and file formats use a non-linear encoding (a gamma compression) of the intended intensities of the primary colors of the photographic reproduction. In addition, the intended reproduction is almost always nonlinearly related to the measured scene intensities, via a tone reproduction nonlinearity.

That is, gamma can be visualized as the slope of the input–output curve when plotted on logarithmic axes. For a power-law curve, this slope is constant, but the idea can be extended to any type of curve, in which case gamma (strictly speaking, "point gamma"

When a photographic film is exposed to light, the result of the exposure can be represented on a graph showing log of exposure on the horizontal axis, and density, or negative log of transmittance, on the vertical axis. For a given film formulation and processing method, this curve is its characteristic or Hurter–Driffield curve.

Output to CRT-based television receivers and monitors does not usually require further gamma correction. The standard video signals that are transmitted or stored in image files incorporate gamma compression matching the gamma expansion of the CRT (although it is not the exact inverse).

For television signals, gamma values are fixed and defined by the analog video standards. CCIR System M and N, associated with NTSC color, use gamma 2.2; the rest (systems B/G, H, I, D/K, K1 and L) associated with PAL or SECAM color, use gamma 2.8.

In most computer display systems, images are encoded with a gamma of about 0.45 and decoded with the reciprocal gamma of 2.2. A notable exception, until the release of Mac OS X 10.6 (Snow Leopard) in September 2009, were Macintosh computers, which encoded with a gamma of 0.55 and decoded with a gamma of 1.8. In any case, binary data in still image files (such as JPEG) are explicitly encoded (that is, they carry gamma-encoded values, not linear intensities), as are motion picture files (such as MPEG). The system can optionally further manage both cases, through color management, if a better match to the output device gamma is required.

Plot of the sRGB standard gamma-expansion nonlinearity in red, and its local gamma value (slope in log–log space) in blue. The local gamma rises from 1 to about 2.2.

The sRGB color space standard used with most cameras, PCs, and printers does not use a simple power-law nonlinearity as above, but has a decoding gamma value near 2.2 over much of its range, as shown in the plot to the right. Below a compressed value of 0.04045 or a linear intensity of 0.00313, the curve is linear (encoded value proportional to intensity), so γ = 1. The dashed black curve behind the red curve is a standard γ = 2.2 power-law curve, for comparison.

Gamma correction in computers is used, for example, to display a gamma = 1.8 Apple picture correctly on a gamma = 2.2 PC monitor by changing the image gamma. Another usage is equalizing of the individual color-channel gammas to correct for monitor discrepancies.

Some picture formats allow an image"s intended gamma (of transformations between encoded image samples and light output) to be stored as metadata, facilitating automatic gamma correction as long as the display system"s exponent is known. The PNG specification includes the gAMA chunk for this purposeJPEG and TIFF the Exif Gamma tag can be used.

These features have historically caused problems, especially on the web. There is no numerical value of gamma that matches the "show the 8-bit numbers unchanged" method used for JPG, GIF, HTML, and CSS colors, so the PNG would not match.Google Chrome (and all other Chromium-based browsers) and Mozilla Firefox either ignore the gamma setting entirely, or ignore it when set to known wrong values.

A gamma characteristic is a power-law relationship that approximates the relationship between the encoded luma in a television system and the actual desired image luminance.

With this nonlinear relationship, equal steps in encoded luminance correspond roughly to subjectively equal steps in brightness. Ebner and Fairchildused an exponent of 0.43 to convert linear intensity into lightness (luma) for neutrals; the reciprocal, approximately 2.33 (quite close to the 2.2 figure cited for a typical display subsystem), was found to provide approximately optimal perceptual encoding of grays.

The following illustration shows the difference between a scale with linearly-increasing encoded luminance signal (linear gamma-compressed luma input) and a scale with linearly-increasing intensity scale (linear luminance output).

On most displays (those with gamma of about 2.2), one can observe that the linear-intensity scale has a large jump in perceived brightness between the intensity values 0.0 and 0.1, while the steps at the higher end of the scale are hardly perceptible. The gamma-encoded scale, which has a nonlinearly-increasing intensity, will show much more even steps in perceived brightness.

A cathode ray tube (CRT), for example, converts a video signal to light in a nonlinear way, because the electron gun"s intensity (brightness) as a function of applied video voltage is nonlinear. The light intensity I is related to the source voltage Vs according to

where γ is the Greek letter gamma. For a CRT, the gamma that relates brightness to voltage is usually in the range 2.35 to 2.55; video look-up tables in computers usually adjust the system gamma to the range 1.8 to 2.2,

For simplicity, consider the example of a monochrome CRT. In this case, when a video signal of 0.5 (representing a mid-gray) is fed to the display, the intensity or brightness is about 0.22 (resulting in a mid-gray, about 22% the intensity of white). Pure black (0.0) and pure white (1.0) are the only shades that are unaffected by gamma.

To compensate for this effect, the inverse transfer function (gamma correction) is sometimes applied to the video signal so that the end-to-end response is linear. In other words, the transmitted signal is deliberately distorted so that, after it has been distorted again by the display device, the viewer sees the correct brightness. The inverse of the function above is

where Vc is the corrected voltage, and Vs is the source voltage, for example, from an image sensor that converts photocharge linearly to a voltage. In our CRT example 1/γ is 1/2.2 ≈ 0.45.

A color CRT receives three video signals (red, green, and blue) and in general each color has its own value of gamma, denoted γR, γG or γB. However, in simple display systems, a single value of γ is used for all three colors.

Other display devices have different values of gamma: for example, a Game Boy Advance display has a gamma between 3 and 4 depending on lighting conditions. In LCDs such as those on laptop computers, the relation between the signal voltage Vs and the intensity I is very nonlinear and cannot be described with gamma value. However, such displays apply a correction onto the signal voltage in order to approximately get a standard γ = 2.5 behavior. In NTSC television recording, γ = 2.2.

The power-law function, or its inverse, has a slope of infinity at zero. This leads to problems in converting from and to a gamma colorspace. For this reason most formally defined colorspaces such as sRGB will define a straight-line segment near zero and add raising x + K (where K is a constant) to a power so the curve has continuous slope. This straight line does not represent what the CRT does, but does make the rest of the curve more closely match the effect of ambient light on the CRT. In such expressions the exponent is not the gamma; for instance, the sRGB function uses a power of 2.4 in it, but more closely resembles a power-law function with an exponent of 2.2, without a linear portion.

Up to four elements can be manipulated in order to achieve gamma encoding to correct the image to be shown on a typical 2.2- or 1.8-gamma computer display:

The pixel"s intensity values in a given image file; that is, the binary pixel values are stored in the file in such way that they represent the light intensity via gamma-compressed values instead of a linear encoding. This is done systematically with digital video files (as those in a DVD movie), in order to minimize the gamma-decoding step while playing, and maximize image quality for the given storage. Similarly, pixel values in standard image file formats are usually gamma-compensated, either for sRGB gamma (or equivalent, an approximation of typical of legacy monitor gammas), or according to some gamma specified by metadata such as an ICC profile. If the encoding gamma does not match the reproduction system"s gamma, further correction may be done, either on display or to create a modified image file with a different profile.

The rendering software writes gamma-encoded pixel binary values directly to the video memory (when highcolor/truecolor modes are used) or in the CLUT hardware registers (when indexed color modes are used) of the display adapter. They drive Digital-to-Analog Converters (DAC) which output the proportional voltages to the display. For example, when using 24-bit RGB color (8 bits per channel), writing a value of 128 (rounded midpoint of the 0–255 byte range) in video memory it outputs the proportional ≈ 0.5 voltage to the display, which it is shown darker due to the monitor behavior. Alternatively, to achieve ≈ 50% intensity, a gamma-encoded look-up table can be applied to write a value near to 187 instead of 128 by the rendering software.

Modern display adapters have dedicated calibrating CLUTs, which can be loaded once with the appropriate gamma-correction look-up table in order to modify the encoded signals digitally before the DACs that output voltages to the monitor.hardware calibration.

Some modern monitors allow the user to manipulate their gamma behavior (as if it were merely another brightness/contrast-like setting), encoding the input signals by themselves before they are displayed on screen. This is also a calibration by hardware technique but it is performed on the analog electric signals instead of remapping the digital values, as in the previous cases.

In a typical system, for example from camera through JPEG file to display, the role of gamma correction will involve several cooperating parts. The camera encodes its rendered image into the JPEG file using one of the standard gamma values such as 2.2, for storage and transmission. The display computer may use a color management engine to convert to a different color space (such as older Macintosh"s γ = 1.8 color space) before putting pixel values into its video memory. The monitor may do its own gamma correction to match the CRT gamma to that used by the video system. Coordinating the components via standard interfaces with default standard gamma values makes it possible to get such system properly configured.

This procedure is useful for making a monitor display images approximately correctly, on systems in which profiles are not used (for example, the Firefox browser prior to version 3.0 and many others) or in systems that assume untagged source images are in the sRGB colorspace.

In the test pattern, the intensity of each solid color bar is intended to be the average of the intensities in the surrounding striped dither; therefore, ideally, the solid areas and the dithers should appear equally bright in a system properly adjusted to the indicated gamma.

Normally a graphics card has contrast and brightness control and a transmissive LCD monitor has contrast, brightness, and backlight control. Graphics card and monitor contrast and brightness have an influence on effective gamma, and should not be changed after gamma correction is completed.

Given a desired display-system gamma, if the observer sees the same brightness in the checkered part and in the homogeneous part of every colored area, then the gamma correction is approximately correct.

Before gamma correction the desired gamma and color temperature should be set using the monitor controls. Using the controls for gamma, contrast and brightness, the gamma correction on an LCD can only be done for one specific vertical viewing angle, which implies one specific horizontal line on the monitor, at one specific brightness and contrast level. An ICC profile allows one to adjust the monitor for several brightness levels. The quality (and price) of the monitor determines how much deviation of this operating point still gives a satisfactory gamma correction. Twisted nematic (TN) displays with 6-bit color depth per primary color have lowest quality. In-plane switching (IPS) displays with typically 8-bit color depth are better. Good monitors have 10-bit color depth, have hardware color management and allow hardware calibration with a tristimulus colorimeter. Often a 6bit plus FRC panel is sold as 8bit and a 8bit plus FRC panel is sold as 10bit. FRC is no true replacement for more bits. The 24-bit and 32-bit color depth formats have 8 bits per primary color.

With Microsoft Windows 7 and above the user can set the gamma correction through the display color calibration tool dccw.exe or other programs.ICC profile file and load it as default. This makes color management easy.color Look Up Table correctly after waking up from standby or hibernate mode and show wrong gamma. In this case update the graphics card driver.

On some operating systems running the X Window System, one can set the gamma correction factor (applied to the existing gamma value) by issuing the command xgamma -gamma 0.9 for setting gamma correction factor to 0.9, and xgamma for querying current value of that factor (the default is 1.0). In macOS systems, the gamma and other related screen calibrations are made through the System Preferences.

The test image is only valid when displayed "raw", i.e. without scaling (1:1 pixel to screen) and color adjustment, on the screen. It does, however, also serve to point out another widespread problem in software: many programs perform scaling in a color space with gamma, instead of a physically-correct linear space. In a sRGB color space with an approximate gamma of 2.2, the image should show a "2.2" result at 50% size, if the zooming is done linearly. Jonas Berlin has created a "your scaling software sucks/rules" image based on the same principle.

In addition to scaling, the problem also applies to other forms of downsampling (scaling down), such as chroma subsampling in JPEG"s gamma-enabled Y′CbCr.WebP solves this problem by calculating the chroma averages in linear space then converting back to a gamma-enabled space; an iterative solution is used for larger images. The same "sharp YUV" (formerly "smart YUV") code is used in sjpeg. Kornelski provides a simpler approximation by luma-based weighted average.Alpha compositing, color gradients, and 3D rendering are also affected by this issue.

Paradoxically, when upsampling (scaling up) an image, the result processed in the "wrong" gamma-enabled space tends to be more aesthetically pleasing. This is because upscaling filters are tuned to minimize the ringing artifacts in a linear space, but human perception is non-linear and better approximated by gamma. An alternative way to trim the artifacts is using a sigmoidal light transfer function, a technique pioneered by GIMP"s LoHalo filter and later adopted by madVR.

The term intensity refers strictly to the amount of light that is emitted per unit of time and per unit of surface, in units of lux. Note, however, that in many fields of science this quantity is called luminous exitance, as opposed to luminous intensity, which is a different quantity. These distinctions, however, are largely irrelevant to gamma compression, which is applicable to any sort of normalized linear intensity-like scale.

One contrasts relative luminance in the sense of color (no gamma compression) with luma in the sense of video (with gamma compression), and denote relative luminance by Y and luma by Y′, the prime symbol (′) denoting gamma compression.

Gamma correction is a type of power law function whose exponent is the Greek letter gamma (γ). It should not be confused with the mathematical Gamma function. The lower case gamma, γ, is a parameter of the former; the upper case letter, Γ, is the name of (and symbol used for) the latter (as in Γ(x)). To use the word "function" in conjunction with gamma correction, one may avoid confusion by saying "generalized power law function".

Without context, a value labeled gamma might be either the encoding or the decoding value. Caution must be taken to correctly interpret the value as that to be applied-to-compensate or to be compensated-by-applying its inverse. In common parlance, in many occasions the decoding value (as 2.2) is employed as if it were the encoding value, instead of its inverse (1/2.2 in this case), which is the real value that must be applied to encode gamma.

McKesson, Jason L. "Chapter 12. Dynamic Range – Linearity and Gamma". Learning Modern 3D Graphics Programming. Archived from the original on 18 July 2013. Retrieved 11 July 2013.

"11A: Characteristics of systems for monochrome and color television". Reports of the CCIR, 1990: Also Decisions : XVIIth Plenary Assembly, Dusseldorf (PDF). International Radio Consultative Committee. 1990.

Fritz Ebner and Mark D Fairchild, "Development and testing of a color space (IPT) with improved hue uniformity," Proceedings of IS&T/SID"s Sixth Color Imaging Conference, p 8-13 (1998).

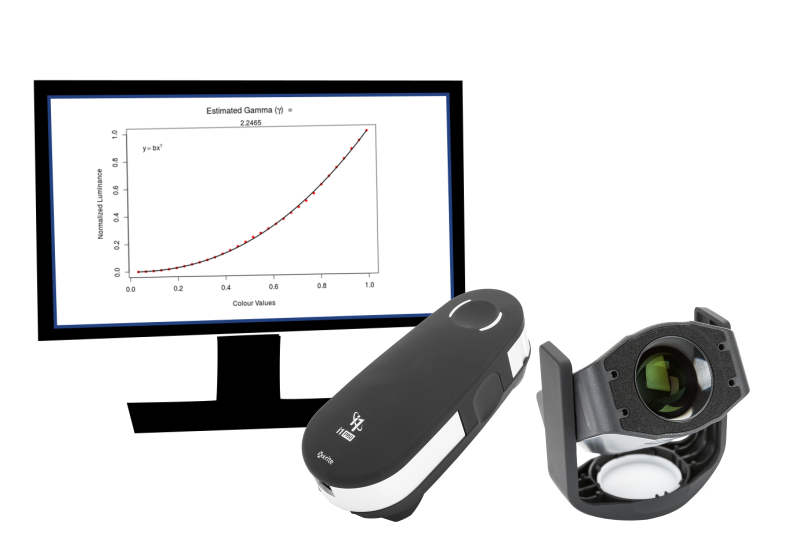
Koren, Norman. "Monitor calibration and gamma". Retrieved 2018-12-10. The chart below enables you to set the black level (brightness) and estimate display gamma over a range of 1 to 3 with precison better than 0.1.

Nienhuys, Han-Kwang (2008). "Gamma calibration". Retrieved 2018-11-30. The reason for using 48% rather than 50% as a luminance is that many LCD screens have saturation issues in the last 5 percent of their brightness range that would distort the gamma measurement.

Andrews, Peter. "The Monitor calibration and Gamma assessment page". Retrieved 2018-11-30. the problem is caused by the risetime of most monitor hardware not being sufficiently fast to turn from full black to full white in the space of a single pixel, or even two, in some cases.

Werle, Eberhard. "Quickgamma". Retrieved 2018-12-10. QuickGamma is a small utility program to calibrate a monitor on the fly without having to buy expensive hardware tools.

As soon as we compute the final pixel colors of the scene we will have to display them on a monitor. In the old days of digital imaging most monitors were cathode-ray tube (CRT) monitors. These monitors had the physical property that twice the input voltage did not result in twice the amount of brightness. Doubling the input voltage resulted in a brightness equal to an exponential relationship of roughly 2.2 known as the gamma of a monitor. This happens to (coincidently) also closely match how human beings measure brightness as brightness is also displayed with a similar (inverse) power relationship. To better understand what this all means take a look at the following image:

The top line looks like the correct brightness scale to the human eye, doubling the brightness (from 0.1 to 0.2 for example) does indeed look like it"s twice as bright with nice consistent differences. However, when we"re talking about the physical brightness of light e.g. amount of photons leaving a light source, the bottom scale actually displays the correct brightness. At the bottom scale, doubling the brightness returns the correct physical brightness, but since our eyes perceive brightness differently (more susceptible to changes in dark colors) it looks weird.

Because the human eyes prefer to see brightness colors according to the top scale, monitors (still today) use a power relationship for displaying output colors so that the original physical brightness colors are mapped to the non-linear brightness colors in the top scale.

This non-linear mapping of monitors does output more pleasing brightness results for our eyes, but when it comes to rendering graphics there is one issue: all the color and brightness options we configure in our applications are based on what we perceive from the monitor and thus all the options are actually non-linear brightness/color options. Take a look at the graph below:

The dotted line represents color/light values in linear space and the solid line represents the color space that monitors display. If we double a color in linear space, its result is indeed double the value. For instance, take a light"s color vector (0.5, 0.0, 0.0) which represents a semi-dark red light. If we would double this light in linear space it would become (1.0, 0.0, 0.0) as you can see in the graph. However, the original color gets displayed on the monitor as (0.218, 0.0, 0.0) as you can see from the graph. Here"s where the issues start to rise: once we double the dark-red light in linear space, it actually becomes more than 4.5 times as bright on the monitor!

Up until this chapter we have assumed we were working in linear space, but we"ve actually been working in the monitor"s output space so all colors and lighting variables we configured weren"t physically correct, but merely looked (sort of) right on our monitor. For this reason, we (and artists) generally set lighting values way brighter than they should be (since the monitor darkens them) which as a result makes most linear-space calculations incorrect. Note that the monitor (CRT) and linear graph both start and end at the same position; it is the intermediate values that are darkened by the display.

You can see that with gamma correction, the (updated) color values work more nicely together and darker areas show more details. Overall, a better image quality with a few small modifications.

Without properly correcting this monitor gamma, the lighting looks wrong and artists will have a hard time getting realistic and good-looking results. The solution is to apply gamma correction.

The idea of gamma correction is to apply the inverse of the monitor"s gamma to the final output color before displaying to the monitor. Looking back at the gamma curve graph earlier this chapter we see another dashed line that is the inverse of the monitor"s gamma curve. We multiply each of the linear output colors by this inverse gamma curve (making them brighter) and as soon as the colors are displayed on the monitor, the monitor"s gamma curve is applied and the resulting colors become linear. We effectively brighten the intermediate colors so that as soon as the monitor darkens them, it balances all out.

Let"s give another example. Say we again have the dark-red color \((0.5, 0.0, 0.0)\). Before displaying this color to the monitor we first apply the gamma correction curve to the color value. Linear colors displayed by a monitor are roughly scaled to a power of \(2.2\) so the inverse requires scaling the colors by a power of \(1/2.2\). The gamma-corrected dark-red color thus becomes \((0.5, 0.0, 0.0)^{1/2.2} = (0.5, 0.0, 0.0)^{0.45} = (0.73, 0.0, 0.0)\). The corrected colors are then fed to the monitor and as a result the color is displayed as \((0.73, 0.0, 0.0)^{2.2} = (0.5, 0.0, 0.0)\). You can see that by using gamma-correction, the monitor now finally displays the colors as we linearly set them in the application.

A gamma value of 2.2 is a default gamma value that roughly estimates the average gamma of most displays. The color space as a result of this gamma of 2.2 is called the sRGB color space (not 100% exact, but close). Each monitor has their own gamma curves, but a gamma value of 2.2 gives good results on most monitors. For this reason, games often allow players to change the game"s gamma setting as it varies slightly per monitor.

The first option is probably the easiest, but also gives you less control. By enabling GL_FRAMEBUFFER_SRGB you tell OpenGL that each subsequent drawing command should first gamma correct colors (from the sRGB color space) before storing them in color buffer(s). The sRGB is a color space that roughly corresponds to a gamma of 2.2 and a standard for most devices. After enabling GL_FRAMEBUFFER_SRGB, OpenGL automatically performs gamma correction after each fragment shader run to all subsequent framebuffers, including the default framebuffer.

From now on your rendered images will be gamma corrected and as this is done by the hardware it is completely free. Something you should keep in mind with this approach (and the other approach) is that gamma correction (also) transforms the colors from linear space to non-linear space so it is very important you only do gamma correction at the last and final step. If you gamma-correct your colors before the final output, all subsequent operations on those colors will operate on incorrect values. For instance, if you use multiple framebuffers you probably want intermediate results passed in between framebuffers to remain in linear-space and only have the last framebuffer apply gamma correction before being sent to the monitor.

The second approach requires a bit more work, but also gives us complete control over the gamma operations. We apply gamma correction at the end of each relevant fragment shader run so the final colors end up gamma corrected before being sent out to the monitor:

The last line of code effectively raises each individual color component of fragColor to 1.0/gamma, correcting the output color of this fragment shader run.

An issue with this approach is that in order to be consistent you have to apply gamma correction to each fragment shader that contributes to the final output. If you have a dozen fragment shaders for multiple objects, you have to add the gamma correction code to each of these shaders. An easier solution would be to introduce a post-processing stage in your render loop and apply gamma correction on the post-processed quad as a final step which you"d only have to do once.

That one line represents the technical implementation of gamma correction. Not all too impressive, but there are a few extra things you have to consider when doing gamma correction.

Because monitors display colors with gamma applied, whenever you draw, edit, or paint a picture on your computer you are picking colors based on what you see on the monitor. This effectively means all the pictures you create or edit are not in linear space, but in sRGB space e.g. doubling a dark-red color on your screen based on perceived brightness, does not equal double the red component.

As a result, when texture artists create art by eye, all the textures" values are in sRGB space so if we use those textures as they are in our rendering application we have to take this into account. Before we knew about gamma correction this wasn"t really an issue, because the textures looked good in sRGB space which is the same space we worked in; the textures were displayed exactly as they are which was fine. However, now that we"re displaying everything in linear space, the texture colors will be off as the following image shows:

The texture image is way too bright and this happens because it is actually gamma corrected twice! Think about it, when we create an image based on what we see on the monitor, we effectively gamma correct the color values of an image so that it looks right on the monitor. Because we then again gamma correct in the renderer, the image ends up way too bright.

The other solution is to re-correct or transform these sRGB textures to linear space before doing any calculations on their color values. We can do this as follows:

To do this for each texture in sRGB space is quite troublesome though. Luckily OpenGL gives us yet another solution to our problems by giving us the GL_SRGB and GL_SRGB_ALPHA internal texture formats.

If we create a texture in OpenGL with any of these two sRGB texture formats, OpenGL will automatically correct the colors to linear-space as soon as we use them, allowing us to properly work in linear space. We can specify a texture as an sRGB texture as follows:

You should be careful when specifying your textures in sRGB space as not all textures will actually be in sRGB space. Textures used for coloring objects (like diffuse textures) are almost always in sRGB space. Textures used for retrieving lighting parameters (like specular maps and normal maps) are almost always in linear space, so if you were to configure these as sRGB textures the lighting will look odd. Be careful in which textures you specify as sRGB.

With our diffuse textures specified as sRGB textures you get the visual output you"d expect again, but this time everything is gamma corrected only once.

Something else that"s different with gamma correction is lighting attenuation. In the real physical world, lighting attenuates closely inversely proportional to the squared distance from a light source. In normal English it simply means that the light strength is reduced over the distance to the light source squared, like below:

However, when using this equation the attenuation effect is usually way too strong, giving lights a small radius that doesn"t look physically right. For that reason other attenuation functions were used (like we discussed in the basic lighting chapter) that give much more control, or the linear equivalent is used:

The linear equivalent gives more plausible results compared to its quadratic variant without gamma correction, but when we enable gamma correction the linear attenuation looks too weak and the physically correct quadratic attenuation suddenly gives the better results. The image below shows the differences:

The cause of this difference is that light attenuation functions change brightness, and as we weren"t visualizing our scene in linear space we chose the attenuation functions that looked best on our monitor, but weren"t physically correct. Think of the squared attenuation function: if we were to use this function without gamma correction, the attenuation function effectively becomes: \((1.0 / distance^2)^{2.2}\) when displayed on a monitor. This creates a much larger attenuation from what we originally anticipated. This also explains why the linear equivalent makes much more sense without gamma correction as this effectively becomes \((1.0 / distance)^{2.2} = 1.0 / distance^{2.2}\) which resembles its physical equivalent a lot more.

The more advanced attenuation function we discussed in the basic lighting chapter still has its place in gamma corrected scenes as it gives more control over the exact attenuation (but of course requires different parameters in a gamma corrected scene).

You can find the source code of this simple demo scene here. By pressing the spacebar we switch between a gamma corrected and un-corrected scene with both scenes using their texture and attenuation equivalents. It"s not the most impressive demo, but it does show how to actually apply all techniques.

To summarize, gamma correction allows us to do all our shader/lighting calculations in linear space. Because linear space makes sense in the physical world, most physical equations now actually give good results (like real light attenuation). The more advanced your lighting becomes, the easier it is to get good looking (and realistic) results with gamma correction. That is also why it"s advised to only really tweak your lighting parameters as soon as you have gamma correction in place.

Every image is encoded with a color profile. Most color profiles do have a gamma correction, but not every color profile has that (raw for example). Most images on the internet are encoded in sRGB, which is gamma corrected. If you would download a random image from the internet, you will more than likely have an image that is in sRGB and thus gamma corrected.

The monitor receives its image in the color profile of the monitor (let"s just say sRGB), it then decodes the image from sRGB to the actual intensity of the pixels and then displays it. Basically, the monitor receives a gamma corrected image and removes the gamma correction just before it displays it.

Images that are saved to a file or that are sent to the monitor, are generally gamma corrected. This is for a very simple reason. We only have 256 values per RGB component to define the color of a pixel. Our eyes are very good at picking up small differences in dark parts of an image, but relatively terrible at picking up small differences in bright parts.

If we try to save an image without any gamma correcting as an 8-bit image (thus 256 values per RGB component), we end up with having the same amount of precision for dark parts in the image and bright parts in the image. However, our eyes cannot see small differences in bright parts of the image, so all that precision in the bright parts is simply wasted. Gamma correction fixes this. Before we convert the image to 8 bits, we first gamma correct it so that we allocate more precision to that darker parts of the image than the brighter parts of the image. When displayed, the monitor will remove that gamma correction.

Left is an image that was gamma corrected before being saved to 8 bits and right is an image that was not gamma corrected before 8 bits. You can clearly see the lack of precision in the darker parts without gamma correction, but not in the bright parts.

This website is using a security service to protect itself from online attacks. The action you just performed triggered the security solution. There are several actions that could trigger this block including submitting a certain word or phrase, a SQL command or malformed data.

We want you to be confident that you’re getting the best price. We’ll match any local competitor’s published price for the same repair and beat it by $5.

uBreakiFix is the nationwide leader in professional same-day electronics repairs - including iPhone, Samsung, Computer, Macs, iPads and other tablet and cell phones. Our professionally trained and certified technicians provide fast and affordable iPhone repairs, cell phone screen replacements and all fixes for PCs, Macs and tablets. With 834 locations in all, we have more than a decade of experience diagnosing and fixing everything from Samsung repairs to iPad screen replacements.

At uBreakiFix, we lead the industry in cell phone repair and computer replacements because of our reliability, affordability and quality service. No other team has a more rigorous training and certification process, and our team is able to fix electronic issues that are not even found by the average repair technician. That"s why we"re comfortable offering a 1 year warranty and pricing guarantee - we stand by the quality of our same-day repair. Whether we"re fixing your iPhone, Samsung, PC or Mac, we will make it work like it"s a brand-new device just taken out of the box.

All customers who add an eligible Banana Pudding Week sale SKU for nationwide U.S. shipping orders only to their cart and checkout on Mag