gamma correction for lcd monitors brands

Problems like extremely poor display of shadow areas, blown-out highlights, or images prepared on Macs appearing too dark on Windows computers are often due to gamma characteristics. In this session, we"ll discuss gamma, which has a significant impact on color reproduction on LCD monitors. Understanding gamma is useful in both color management and product selection. Users who value picture quality are advised to check this information.

* Below is the translation from the Japanese of the ITmedia article "Is the Beauty of a Curve Decisive for Color Reproduction? Learning About LCD Monitor Gamma" published July 13, 2009. Copyright 2011 ITmedia Inc. All Rights Reserved.

The term gamma comes from the third letter of the Greek alphabet, written Γ in upper case and γ in lower case. The word gamma occurs often in everyday life, in terms like gamma rays, the star called Gamma Velorum, and gamma-GTP. In computer image processing, the term generally refers to the brightness of intermediate tones (gray).

Let"s discuss gamma in a little more detail. In a PC environment, the hardware used when working with color includes monitors, printers, and scanners. When using these devices connected to a PC, we input and output color information to and from each device. Since each device has its own unique color handling characteristics (or tendencies), color information cannot be output exactly as input. The color handling characteristics that arise in input and output are known as gamma characteristics.

While certain monitors are also compatible with color handling at 10 bits per RGB color (210 = 1024 tones), or 1024 x 3 (approximately 1,064,330,000 colors), operating system and application support for such monitors has lagged. Currently, some 16.77 million colors, with eight bits per RGB color, is the standard color environment for PC monitors.

When a PC and a monitor exchange color information, the ideal is a relationship in which the eight-bit color information per RGB color input from the PC to the monitor can be output accurately—that is, a 1:1 relationship for input:output. However, since gamma characteristics differ between PCs and monitors, color information is not transmitted according to a 1:1 input:output relationship.

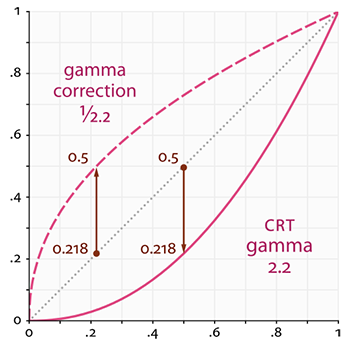
How colors ultimately look depends on the relationship resulting from the gamma values (γ) that numerically represent the gamma characteristics of each hardware device. If the color information input is represented as x and output as y, the relationship applying the gamma value can be represented by the equation y = xγ.

Gamma characteristics are represented by the equation y = xγ. At the ideal gamma value of 1.0, y = x; but since each monitor has its own unique gamma characteristics (gamma values), y generally doesn"t equal x. The above graph depicts a curve adjusted to the standard Windows gamma value of 2.2. The standard gamma value for the Mac OS is 1.8.

Ordinarily, the nature of monitor gamma is such that intermediate tones tend to appear dark. Efforts seek to promote accurate exchange of color information by inputting data signals in which the intermediate tones have already been brightened to approach an input:output balance of 1:1. Balancing color information to match device gamma characteristics in this way is called gamma correction.

A simple gamma correction system. If we account for monitor gamma characteristics and input color information with gamma values adjusted accordingly (i.e., color information with intermediate tones brightened), color handling approaches the y = x ideal. Since gamma correction generally occurs automatically, users usually obtain correct color handling on a PC monitor without much effort. However, the precision of gamma correction varies from manufacturer to manufacturer and from product to product (see below for details).

In most cases, if a computer runs the Windows operating system, we can achieve close to ideal colors by using a monitor with a gamma value of 2.2. This is because Windows assumes a monitor with a gamma value of 2.2, the standard gamma value for Windows. Most LCD monitors are designed based on a gamma value of 2.2.

The standard monitor gamma value for the Mac OS is 1.8. The same concept applies as in Windows. We can obtain color reproduction approaching the ideal by connecting a Mac to a monitor configured with a gamma value of 1.8.

An example of the same image displayed at gamma values of 2.2 (photo at left) and 1.8 (photo at right). At a gamma value of 1.8, the overall image appears brighter. The LCD monitor used is EIZO"s 20-inch wide-screen EV2023W FlexScan model (ITmedia site).

To equalize color handling in mixed Windows and Mac environments, it"s a good idea to standardize the gamma values between the two operating systems. Changing the gamma value for the Mac OS is easy; but Windows provides no such standard feature. Since Windows users perform color adjustments through the graphics card driver or separate color-adjustment software, changing the gamma value can be an unexpectedly complex task. If the monitor used in a Windows environment offers a feature for adjusting gamma values, obtaining more accurate results will likely be easier.

If we know that a certain image was created in a Mac OS environment with a gamma value of 1.8, or if an image received from a Mac user appears unnaturally dark, changing the monitor gamma setting to 1.8 should show the image with the colors intended by the creator.

Eizo Nanao"s LCD monitors allow users to configure the gamma value from the OSD menu, making this procedure easy. In addition to the initially configured gamma value of 2.2., one can choose from multiple settings, including the Mac OS standard of 1.8.

To digress slightly, standard gamma values differ between Windows and Mac OS for reasons related to the design concepts and histories of the two operating systems. Windows adopted a gamma value corresponding to television (2.2), while the Mac OS adopted a gamma value corresponding to commercial printers (1.8). The Mac OS has a long history of association with commercial printing and desktop publishing applications, for which 1.8 remains the basic gamma value, even now. On the other hand, a gamma value of 2.2 is standard in the sRGB color space, the standard for the Internet and for digital content generally, and for Adobe RGB, the use of which has expanded for wide-gamut printing,.

Given the proliferating use of color spaces like sRGB and Adobe RGB, plans call for the latest Mac OS scheduled for release by Apple Computer in September 2009, Mac OS X 10.6 Snow Leopard, to switch from a default gamma value of 1.8 to 2.2. A gamma value of 2.2 is expected to become the future mainstream for Macs.

On the preceding page, we mentioned that the standard gamma value in a Windows environment is 2.2 and that many LCD monitors can be adjusted to a gamma value of 2.2. However, due to the individual tendencies of LCD monitors (or the LCD panels installed in them), it"s hard to graph a smooth gamma curve of 2.2.

Traditionally, LCD panels have featured S-shaped gamma curves, with ups and downs here and there and curves that diverge by RGB color. This phenomenon is particularly marked for dark and light tones, often appearing to the eye of the user as tone jumps, color deviations, and color breakdown.

The internal gamma correction feature incorporated into LCD monitors that emphasize picture quality allows such irregularity in the gamma curve to be corrected to approach the ideal of y = x γ. Device specs provide one especially useful figure to help us determine whether a monitor has an internal gamma correction feature: A monitor can be considered compatible with internal gamma correction if the figure for maximum number of colors is approximately 1,064,330,000 or 68 billion or if the specs indicate the look-up table (LUT) is 10- or 12-bit.

An internal gamma correction feature applies multi-gradation to colors and reallocates them. While the input from a PC to an LCD monitor is in the form of color information at eight bits per RGB color, within the LCD monitor, multi-gradation is applied to increase this to 10 bits (approximately 1,064,330,000 colors) or 12 bits (approximately 68 billion colors). The optimal color at eight bits per RGB color (approximately 16.77 million colors) is identified by referring to the LUT and displayed on screen. This corrects irregularity in the gamma curve and deviations in each RGB color, causing the output on screen to approach the ideal of y = x γ.

Let"s look at a little more information on the LUT. The LUT is a table containing the results of certain calculations performed in advance. The results for certain calculations can be obtained simply by referring to the LUT, without actually performing the calculations. This accelerates processing and reduces the load on a system. The LUT in an LCD monitor identifies the optimal eight-bit RGB colors from multi-gradation color data of 10 or more bits.

An overview of an internal gamma correction feature. Eight-bit RGB color information input from the PC is subjected to multi-gradation to 10 or more bits. This is then remapped to the optimal eight-bit RGB tone by referring to the LUT. Following internal gamma correction, the results approach the ideal gamma curve, dramatically improving on screen gradation and color reproduction.

Eizo Nanao"s LCD monitors proactively employ internal gamma correction features. In models designed especially for high picture quality and in some models in the ColorEdge series designed for color management, eight-bit RGB input signals from the PC are subjected to multi-gradation, and calculations are performed at 14 or 16 bits. A key reason for performing calculations at bit counts higher than the LUT bit count is to improve gradation still further, particularly the reproduction of darker tones. Users seeking high-quality color reproduction should probably choose a monitor model like this one.

In conclusion, we"ve prepared image patterns that make it easy to check the gamma values of an LCD monitor, based on this session"s discussion. Looking directly at your LCD monitor, move back slightly from the screen and gaze at the following images with your eyes half-closed. Visually compare the square outlines and the stripes around them, looking for patterns that appear to have the same tone of gray (brightness). The pattern for which the square frame and the striped pattern around it appear closest in brightness represents the rough gamma value to which the monitor is currently configured.

Based on a gamma value of 2.2, if the square frame appears dark, the LCD monitor"s gamma value is low. If the square frame appears bright, the gamma value is high. You can adjust the gamma value by changing the LCD monitor"s brightness settings or by adjusting brightness in the driver menu for the graphics card.

Naturally, it"s even easier to adjust the gamma if you use a model designed for gamma value adjustments, like an EIZO LCD monitor. For even better color reproduction, you can set the gamma value and optimize color reproduction by calibrating your monitor.

This Display 101article will explain the basics of display gamma correction. To do that we need to show you some background of the gamma correction screen is applied with. It boils down to signal processing behind displaying content on LCD modules.

The human eye is a complicated organ. It’s worthwhile to know some facts about how the eye processes information. Evolution shaped the modern human eye for thousands of years. There are lots of tricks to achieve the best possible effect. A good example is the fact that our eyes are not very sensitive to changes in the light color areas, but can very easily spot changes in a dark environment.

However, it is not typically the case: the relationship between pixel value and luminance typically follows a positive power function of the form y= xγ, where  y is the normalized luminance value, x the pixel value, and gamma (γ) is the power that characterizes the relationship between the two values. ​

Historically, cathode-ray tube screens (CRTs) were the first types of screens used to visualize video content, and different luminance levels were produced by varying the number of electrons fired from an electron gun. This electron gun responded to voltage input according to a power function of 2.5, known as gamma.

Other display technologies are also non-linear, such as the LCD panels of commercial displays, but also those of the VIEWPixx and VIEWPixx/3D screens. Here are some examples of gamma in visual displays used in vision research:

This non-linear relationship happens to have a very useful practical application in video recording. Indeed, the amount of information that can conveyed through a video signal is typically rather limited, where each colour of an RBG triplet is encoded with 8 bits of information. In other words, the specific amount of red, green and blue of a given pixel can only be set at one of 2^8 = 256 levels, between the minimum and maximum luminance level that a screen can display. However, humans are much more sensitive to small increases of light at low-luminance levels, than they are to similar increases of light at high-light levels. If the relationship between the colour value and the luminance was perfectly linear, then most of the bits used to encode the high-luminances would be essentially wasted, since viewers could not tell the difference between the different values, while there might be very obvious differences at the low-light levels.

It turns out that a CRT response is almost exactly the inverse of human lightness sensitivity, a property that can be neatly exploited in computer graphics. In the early days, it was recognized that if video data was recorded with a transfer function that compresses video signal to maximize human perception, then the CRT could be used to essentially ‘decompress’ the signal, without requiring any further transformation on the video signal. The general principle behind video compression is still used today. Sequence A, below, illustrates the associated process.

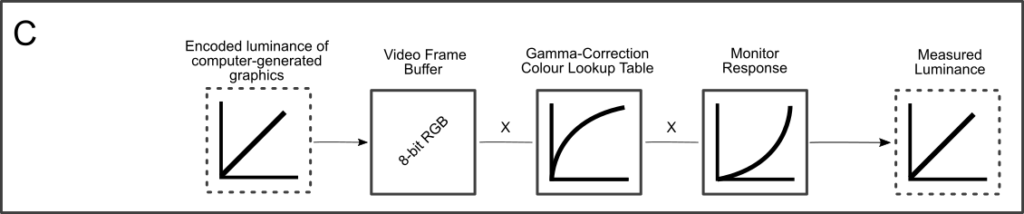
As vision scientists, we typically generate entirely new images and wish to send them directly to the graphic card’s video buffer. However, as seen in Sequence B, below, bypassing an encoding transfer function means that the monitor’s gamma will de-linearize our stimuli, greatly altering our intended stimulus.

For vision scientists, the simplest and most computationally efficient method of applying a gamma correction to our monitor, i.e., of compensating for the monitor’s non-linear response, is to instruct the graphics card to modify the relationship between the pixel input value and the signal that is actually sent to the monitor. To do so, it is possible to apply a custom gamma-correction colour lookup table (gamma-correction CLUT) that is the inverse of the monitor’s gamma.

A colour lookup table (CLUT) is essentially a matrix that converts (or remaps) a pixel value input to a different output, according to your own preference. For an 8-bit RGB video signal, such as the signal typically sent to a VIEWPixx/3D or a VIEWPixx, the CLUT will always take the form of a 28 = 256 row by 3 column matrix, where the rows represent each of the possible colour values the signal can contain, and where the columns correspond to the red, green and blue components of the video signal. For example, in MATLAB and Psychtoolbox, it is expected that each of the cells contains a decimal number ranging from 0 to 1. When applied by the software, this value is converted to a format usable by the display device. On VPixx hardware, this decimal number is stored internally as a 16-bit int.

By default, for each of the 256 levels of an 8-bit video signal, the implicit luminance ramp contains linearly increasing values, uncompensated for any non-linearity in the monitor:

The crux of the problem rests on the practical difficulty of obtaining the proper inverse gamma function and using it to generate the gamma-correction CLUT that should be applied for any given experiment. There are three methods to gamma correct a display:One approach is to simply use the gamma value provided by display manufacturers to generate the gamma-correction CLUT, typically 2.2. This can often be adjusted in the options of advanced graphic cards.

Measure luminance on greyscale luminance patches, encompassing the minimum and maximum pixel values. Apply the resulting gamma equally to all colour channels.

Measure luminance independently for the red, green and blue colour channel, encompassing the minimum and maximum pixel values. Apply the resulting gamma independently to all colour channels.

Practically, greyscale and colour-dependent gamma-correction CLUTs can be obtained with the same procedure:Measure the luminance of your display at equally spaced pixel values, including the minimum and maximum displayed luminance of your screen. A non-linear curve would typically be obtained.

Fit a power function to the experimental data, plot the inverse function, and compute the gamma-correction CLUT values for each of the 256 potential RGB pixel values.

Display non-linearity is not a new problem, and indeed, there are already several tools available online for vision scientists. Notably, for those who use MATLAB and Psychtoolbox, there exists a

Gamma, previously in CRT and early LCD monitors, was directly linked to voltage and was an important factor in reproducing images accurately on displays. In current LCD monitors, Gamma can be thought of as the moderator of the relationship between the brightness of the data captured (input) and how that affects the total human eye perception of color (output) while viewing the display, in terms of color brightness. In a more technical sense, it is the correction of brightness in an image’s color through color shading balance in a pixel‘s value. Pixels have values that range between 0 (black) to 255 (white) with various degrees of grey in between. Our normal vision (not excessively dark or exceedingly bright conditions) is more sensitive to changes in dark tones and due to the capture process of an image, color can be misrepresented, as a result of the difference in how we perceive brightness and the luminance, from when the original image was captured. Our eyes capture brightness in a disproportional way, for example, if a camera captures an image in an extremely bright setting, our eyes perceive the light as being only a fraction brighter. If the image is processed and displayed on a desktop without gamma correction, it will then be perceived by the user as being washed out or too bright. Due to the imbalance, gamma is used to ensure the input relationship matches the desktop output.

When applying this range to color (RGB) colors can be produced at various brightness levels, while not affecting the color hue. A red pixel with a value of 192 would be three quarters of the possible brightness with a red pixel with a value of 10 would be extremely dark. Gamma correction is needed to adjust images in response to the properties of human vision, in order to produce true color. Our eyes capture brightness in a disproportional way, for example, if a camera captures an image and it is exceedingly bright, we will perceive the light as being only a fraction brighter. If the image is processed and displayed on a desktop without gamma correction, it will then be perceived by the user as being washed out or too bright. Due to the brightness imbalance, gamma is used to balance the input relationship to match the desktop output creating true to life color. There are various levels of gamma that can balance color, with varying degrees of success. Gamma levels of 1.8 and 2.2 (Mac OS and Windows OS respectively) were the de facto standard for many years, with gamma level adjustment becoming the new standard in professional monitor production.

Gamma curve importance stems from the need of smooth gradation between colors and color correction. As technology has improved, internal gamma correction features have been incorporated into LCD monitors, which apply multi-gradation to colors and correct the color information. With 10-bit color processing (approximately 1.07 billion colors) and an enhanced LUT processor, screen gradation and color reproduction can be dramatically improved. To improve gradation further, subjugating an eight-bit count input signal to a 14 or 16 bit calculation can help improve the reproduction of darker tones, improve intermediate color gradation and produce higher quality, more precise color output.

Gamma 2.2 has been the standard for Windows and Apple (since Mac OS X v10.6 Snow Leopard). Using a monitor with a gamma level of 2.2 can produce almost optimal colors. This level provides the optimal balance for true color and is used as the standard for graphic and video professionals.

ViewSonic Pre-set Gamma settings: In addition to Gamma 2.2, VP2780-4K also offers Gamma 1.8, Gamma 2.0, Gamma 2.4 and Gamma 2.6 for different kinds of viewing scenarios. This range helps compliment everyday life and viewing situations, whether scenes are too bright and need an enhanced bright color gradient (2.4, 2.6) or too dark (1.8, 2.0). This optimal range allows users the ability to quickly change between modes and find the desired viewing setting for the ideal situation. Whether for casual users, wanting to improve their movie experience or professional movie makers, graphic designers and photographers, ViewSonic Pre-set Gamma settings support a wide range of uses and needs.

Gamma 1.8: Previously the standard for Mac computers, this setting enhances the color gradient between darker tones, not only making darker scenes clearer but also increases overall color tone brightness. This setting is ideal for watching movies, television or situations where scenes or pictures are too dark.

Gamma 2.0:As another option, this gamma setting can offer balance while still providing increased enhancement of dark tones, not only enhancing the detail in darker scenes but also the soft, gentle scenes as well. Originally designed as a compromise for Mac and PC this setting is a perfect middle ground for users that want to utilize the flexibility of multiple gamma settings.

Gamma 2.2:The standard for gamma settings to balance true color with monitors. This gamma setting is the true standard with Windows and Mac fully supported and the most widely used setting. Adopted because of true color output, gamma 2.2 provides the best curve to produce true to life colors with washout or inaccurate shadows.

Gamma 2.4:As an additional choice, this gamma setting is used to enhance the detail in scenes that are slightly too bright, providing increased contrast, and improved visibility of vivid colors. Perfect for HD television production, and the Rec. 709 color space, this gamma setting supports professional users that want to get the most from their high quality Viewsoninc monitors.

Gamma 2.6:This gamma setting is used to highlight bright tonal contrast in pictures and video where differences in brighter tones are harder to perceive. These various settings allow flexibility to the user, to choose which setting is the ideal, depending on the situation. The gamma standard for DCI (Digital Cinema Initiative) and movie production, this setting provides the truest color for users to produce cinema and film.

Every image is encoded with a color profile. Most color profiles do have a gamma correction, but not every color profile has that (raw for example). Most images on the internet are encoded in sRGB, which is gamma corrected. If you would download a random image from the internet, you will more than likely have an image that is in sRGB and thus gamma corrected.

The monitor receives its image in the color profile of the monitor (let"s just say sRGB), it then decodes the image from sRGB to the actual intensity of the pixels and then displays it. Basically, the monitor receives a gamma corrected image and removes the gamma correction just before it displays it.

Images that are saved to a file or that are sent to the monitor, are generally gamma corrected. This is for a very simple reason. We only have 256 values per RGB component to define the color of a pixel. Our eyes are very good at picking up small differences in dark parts of an image, but relatively terrible at picking up small differences in bright parts.

If we try to save an image without any gamma correcting as an 8-bit image (thus 256 values per RGB component), we end up with having the same amount of precision for dark parts in the image and bright parts in the image. However, our eyes cannot see small differences in bright parts of the image, so all that precision in the bright parts is simply wasted. Gamma correction fixes this. Before we convert the image to 8 bits, we first gamma correct it so that we allocate more precision to that darker parts of the image than the brighter parts of the image. When displayed, the monitor will remove that gamma correction.

Left is an image that was gamma corrected before being saved to 8 bits and right is an image that was not gamma corrected before 8 bits. You can clearly see the lack of precision in the darker parts without gamma correction, but not in the bright parts.

Gamma is an important but seldom understood characteristic of virtually all digital imaging systems. It defines the relationship between a pixel"s numerical value and its actual luminance. Without gamma, shades captured by digital cameras wouldn"t appear as they did to our eyes (on a standard monitor). It"s also referred to as gamma correction, gamma encoding or gamma compression, but these all refer to a similar concept. Understanding how gamma works can improve one"s exposure technique, in addition to helping one make the most of image editing.

1. Our eyes do not perceive light the way cameras do. With a digital camera, when twice the number of photons hit the sensor, it receives twice the signal (a "linear" relationship). Pretty logical, right? That"s not how our eyes work. Instead, we perceive twice the light as being only a fraction brighter — and increasingly so for higher light intensities (a "nonlinear" relationship).

Compared to a camera, we are much more sensitive to changes in dark tones than we are to similar changes in bright tones. There"s a biological reason for this peculiarity: it enables our vision to operate over a broader range of luminance. Otherwise the typical range in brightness we encounter outdoors would be too overwhelming.

But how does all of this relate to gamma? In this case, gamma is what translates between our eye"s light sensitivity and that of the camera. When a digital image is saved, it"s therefore "gamma encoded" — so that twice the value in a file more closely corresponds to what we would perceive as being twice as bright.

Technical Note: Gamma is defined by Vout = Vingamma , where Vout is the output luminance value and Vin is the input/actual luminance value. This formula causes the blue line above to curve. When gamma<1, the line arches upward, whereas the opposite occurs with gamma>1.

2. Gamma encoded images store tones more efficiently. Since gamma encoding redistributes tonal levels closer to how our eyes perceive them, fewer bits are needed to describe a given tonal range. Otherwise, an excess of bits would be devoted to describe the brighter tones (where the camera is relatively more sensitive), and a shortage of bits would be left to describe the darker tones (where the camera is relatively less sensitive):

Notice how the linear encoding uses insufficient levels to describe the dark tones — even though this leads to an excess of levels to describe the bright tones. On the other hand, the gamma encoded gradient distributes the tones roughly evenly across the entire range ("perceptually uniform"). This also ensures that subsequent image editing, color and histograms are all based on natural, perceptually uniform tones.

Despite all of these benefits, gamma encoding adds a layer of complexity to the whole process of recording and displaying images. The next step is where most people get confused, so take this part slowly. A gamma encoded image has to have "gamma correction" applied when it is viewed — which effectively converts it back into light from the original scene. In other words, the purpose of gamma encoding is for recording the image — not for displaying the image. Fortunately this second step (the "display gamma") is automatically performed by your monitor and video card. The following diagram illustrates how all of this fits together:

1. Image Gamma. This is applied either by your camera or RAW development software whenever a captured image is converted into a standard JPEG or TIFF file. It redistributes native camera tonal levels into ones which are more perceptually uniform, thereby making the most efficient use of a given bit depth.

2. Display Gamma. This refers to the net influence of your video card and display device, so it may in fact be comprised of several gammas. The main purpose of the display gamma is to compensate for a file"s gamma — thereby ensuring that the image isn"t unrealistically brightened when displayed on your screen. A higher display gamma results in a darker image with greater contrast.

3. System Gamma. This represents the net effect of all gamma values that have been applied to an image, and is also referred to as the "viewing gamma." For faithful reproduction of a scene, this should ideally be close to a straight line (gamma = 1.0). A straight line ensures that the input (the original scene) is the same as the output (the light displayed on your screen or in a print). However, the system gamma is sometimes set slightly greater than 1.0 in order to improve contrast. This can help compensate for limitations due to the dynamic range of a display device, or due to non-ideal viewing conditions and image flare.

The precise image gamma is usually specified by a color profile that is embedded within the file. Most image files use an encoding gamma of 1/2.2 (such as those using sRGB and Adobe RGB 1998 color), but the big exception is with RAW files, which use a linear gamma. However, RAW image viewers typically show these presuming a standard encoding gamma of 1/2.2, since they would otherwise appear too dark:

If no color profile is embedded, then a standard gamma of 1/2.2 is usually assumed. Files without an embedded color profile typically include many PNG and GIF files, in addition to some JPEG images that were created using a "save for the web" setting.

Technical Note on Camera Gamma. Most digital cameras record light linearly, so their gamma is assumed to be 1.0, but near the extreme shadows and highlights this may not hold true. In that case, the file gamma may represent a combination of the encoding gamma and the camera"s gamma. However, the camera"s gamma is usually negligible by comparison. Camera manufacturers might also apply subtle tonal curves, which can also impact a file"s gamma.

This is the gamma that you are controlling when you perform monitor calibration and adjust your contrast setting. Fortunately, the industry has converged on a standard display gamma of 2.2, so one doesn"t need to worry about the pros/cons of different values. Older macintosh computers used a display gamma of 1.8, which made non-mac images appear brighter relative to a typical PC, but this is no longer the case.

Recall that the display gamma compensates for the image file"s gamma, and that the net result of this compensation is the system/overall gamma. For a standard gamma encoded image file (—), changing the display gamma (—) will therefore have the following overall impact (—) on an image:

Recall from before that the image file gamma (—) plus the display gamma (—) equals the overall system gamma (—). Also note how higher gamma values cause the red curve to bend downward.

If you"re having trouble following the above charts, don"t despair! It"s a good idea to first have an understanding of how tonal curves impact image brightness and contrast. Otherwise you can just look at the portrait images for a qualitative understanding.

How to interpret the charts. The first picture (far left) gets brightened substantially because the image gamma (—) is uncorrected by the display gamma (—), resulting in an overall system gamma (—) that curves upward. In the second picture, the display gamma doesn"t fully correct for the image file gamma, resulting in an overall system gamma that still curves upward a little (and therefore still brightens the image slightly). In the third picture, the display gamma exactly corrects the image gamma, resulting in an overall linear system gamma. Finally, in the fourth picture the display gamma over-compensates for the image gamma, resulting in an overall system gamma that curves downward (thereby darkening the image).

The overall display gamma is actually comprised of (i) the native monitor/LCD gamma and (ii) any gamma corrections applied within the display itself or by the video card. However, the effect of each is highly dependent on the type of display device.

CRT Monitors. Due to an odd bit of engineering luck, the native gamma of a CRT is 2.5 — almost the inverse of our eyes. Values from a gamma-encoded file could therefore be sent straight to the screen and they would automatically be corrected and appear nearly OK. However, a small gamma correction of ~1/1.1 needs to be applied to achieve an overall display gamma of 2.2. This is usually already set by the manufacturer"s default settings, but can also be set during monitor calibration.

LCD Monitors. LCD monitors weren"t so fortunate; ensuring an overall display gamma of 2.2 often requires substantial corrections, and they are also much less consistent than CRT"s. LCDs therefore require something called a look-up table (LUT) in order to ensure that input values are depicted using the intended display gamma (amongst other things). See the tutorial on monitor calibration: look-up tables for more on this topic.

Technical Note: The display gamma can be a little confusing because this term is often used interchangeably with gamma correction, since it corrects for the file gamma. However, the values given for each are not always equivalent. Gamma correction is sometimes specified in terms of the encoding gamma that it aims to compensate for — not the actual gamma that is applied. For example, the actual gamma applied with a "gamma correction of 1.5" is often equal to 1/1.5, since a gamma of 1/1.5 cancels a gamma of 1.5 (1.5 * 1/1.5 = 1.0). A higher gamma correction value might therefore brighten the image (the opposite of a higher display gamma).

Dynamic Range. In addition to ensuring the efficient use of image data, gamma encoding also actually increases the recordable dynamic range for a given bit depth. Gamma can sometimes also help a display/printer manage its limited dynamic range (compared to the original scene) by improving image contrast.

Gamma Correction. The term "gamma correction" is really just a catch-all phrase for when gamma is applied to offset some other earlier gamma. One should therefore probably avoid using this term if the specific gamma type can be referred to instead.

Gamma Compression & Expansion. These terms refer to situations where the gamma being applied is less than or greater than one, respectively. A file gamma could therefore be considered gamma compression, whereas a display gamma could be considered gamma expansion.

Applicability. Strictly speaking, gamma refers to a tonal curve which follows a simple power law (where Vout = Vingamma), but it"s often used to describe other tonal curves. For example, the sRGB color space is actually linear at very low luminosity, but then follows a curve at higher luminosity values. Neither the curve nor the linear region follow a standard gamma power law, but the overall gamma is approximated as 2.2.

Is Gamma Required? No, linear gamma (RAW) images would still appear as our eyes saw them — but only if these images were shown on a linear gamma display. However, this would negate gamma"s ability to efficiently record tonal levels.

As soon as we compute the final pixel colors of the scene we will have to display them on a monitor. In the old days of digital imaging most monitors were cathode-ray tube (CRT) monitors. These monitors had the physical property that twice the input voltage did not result in twice the amount of brightness. Doubling the input voltage resulted in a brightness equal to an exponential relationship of roughly 2.2 known as the gamma of a monitor. This happens to (coincidently) also closely match how human beings measure brightness as brightness is also displayed with a similar (inverse) power relationship. To better understand what this all means take a look at the following image:

The top line looks like the correct brightness scale to the human eye, doubling the brightness (from 0.1 to 0.2 for example) does indeed look like it"s twice as bright with nice consistent differences. However, when we"re talking about the physical brightness of light e.g. amount of photons leaving a light source, the bottom scale actually displays the correct brightness. At the bottom scale, doubling the brightness returns the correct physical brightness, but since our eyes perceive brightness differently (more susceptible to changes in dark colors) it looks weird.

Because the human eyes prefer to see brightness colors according to the top scale, monitors (still today) use a power relationship for displaying output colors so that the original physical brightness colors are mapped to the non-linear brightness colors in the top scale.

This non-linear mapping of monitors does output more pleasing brightness results for our eyes, but when it comes to rendering graphics there is one issue: all the color and brightness options we configure in our applications are based on what we perceive from the monitor and thus all the options are actually non-linear brightness/color options. Take a look at the graph below:

The dotted line represents color/light values in linear space and the solid line represents the color space that monitors display. If we double a color in linear space, its result is indeed double the value. For instance, take a light"s color vector (0.5, 0.0, 0.0) which represents a semi-dark red light. If we would double this light in linear space it would become (1.0, 0.0, 0.0) as you can see in the graph. However, the original color gets displayed on the monitor as (0.218, 0.0, 0.0) as you can see from the graph. Here"s where the issues start to rise: once we double the dark-red light in linear space, it actually becomes more than 4.5 times as bright on the monitor!

Up until this chapter we have assumed we were working in linear space, but we"ve actually been working in the monitor"s output space so all colors and lighting variables we configured weren"t physically correct, but merely looked (sort of) right on our monitor. For this reason, we (and artists) generally set lighting values way brighter than they should be (since the monitor darkens them) which as a result makes most linear-space calculations incorrect. Note that the monitor (CRT) and linear graph both start and end at the same position; it is the intermediate values that are darkened by the display.

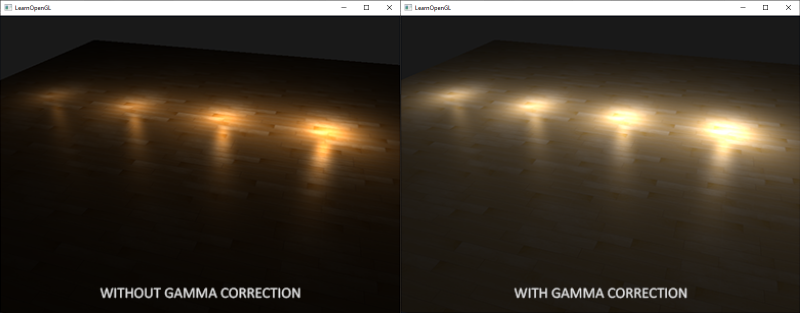
You can see that with gamma correction, the (updated) color values work more nicely together and darker areas show more details. Overall, a better image quality with a few small modifications.

Without properly correcting this monitor gamma, the lighting looks wrong and artists will have a hard time getting realistic and good-looking results. The solution is to apply gamma correction.

The idea of gamma correction is to apply the inverse of the monitor"s gamma to the final output color before displaying to the monitor. Looking back at the gamma curve graph earlier this chapter we see another dashed line that is the inverse of the monitor"s gamma curve. We multiply each of the linear output colors by this inverse gamma curve (making them brighter) and as soon as the colors are displayed on the monitor, the monitor"s gamma curve is applied and the resulting colors become linear. We effectively brighten the intermediate colors so that as soon as the monitor darkens them, it balances all out.

Let"s give another example. Say we again have the dark-red color \((0.5, 0.0, 0.0)\). Before displaying this color to the monitor we first apply the gamma correction curve to the color value. Linear colors displayed by a monitor are roughly scaled to a power of \(2.2\) so the inverse requires scaling the colors by a power of \(1/2.2\). The gamma-corrected dark-red color thus becomes \((0.5, 0.0, 0.0)^{1/2.2} = (0.5, 0.0, 0.0)^{0.45} = (0.73, 0.0, 0.0)\). The corrected colors are then fed to the monitor and as a result the color is displayed as \((0.73, 0.0, 0.0)^{2.2} = (0.5, 0.0, 0.0)\). You can see that by using gamma-correction, the monitor now finally displays the colors as we linearly set them in the application.

A gamma value of 2.2 is a default gamma value that roughly estimates the average gamma of most displays. The color space as a result of this gamma of 2.2 is called the sRGB color space (not 100% exact, but close). Each monitor has their own gamma curves, but a gamma value of 2.2 gives good results on most monitors. For this reason, games often allow players to change the game"s gamma setting as it varies slightly per monitor.

The first option is probably the easiest, but also gives you less control. By enabling GL_FRAMEBUFFER_SRGB you tell OpenGL that each subsequent drawing command should first gamma correct colors (from the sRGB color space) before storing them in color buffer(s). The sRGB is a color space that roughly corresponds to a gamma of 2.2 and a standard for most devices. After enabling GL_FRAMEBUFFER_SRGB, OpenGL automatically performs gamma correction after each fragment shader run to all subsequent framebuffers, including the default framebuffer.

From now on your rendered images will be gamma corrected and as this is done by the hardware it is completely free. Something you should keep in mind with this approach (and the other approach) is that gamma correction (also) transforms the colors from linear space to non-linear space so it is very important you only do gamma correction at the last and final step. If you gamma-correct your colors before the final output, all subsequent operations on those colors will operate on incorrect values. For instance, if you use multiple framebuffers you probably want intermediate results passed in between framebuffers to remain in linear-space and only have the last framebuffer apply gamma correction before being sent to the monitor.

The second approach requires a bit more work, but also gives us complete control over the gamma operations. We apply gamma correction at the end of each relevant fragment shader run so the final colors end up gamma corrected before being sent out to the monitor:

The last line of code effectively raises each individual color component of fragColor to 1.0/gamma, correcting the output color of this fragment shader run.

An issue with this approach is that in order to be consistent you have to apply gamma correction to each fragment shader that contributes to the final output. If you have a dozen fragment shaders for multiple objects, you have to add the gamma correction code to each of these shaders. An easier solution would be to introduce a post-processing stage in your render loop and apply gamma correction on the post-processed quad as a final step which you"d only have to do once.

That one line represents the technical implementation of gamma correction. Not all too impressive, but there are a few extra things you have to consider when doing gamma correction.

Because monitors display colors with gamma applied, whenever you draw, edit, or paint a picture on your computer you are picking colors based on what you see on the monitor. This effectively means all the pictures you create or edit are not in linear space, but in sRGB space e.g. doubling a dark-red color on your screen based on perceived brightness, does not equal double the red component.

As a result, when texture artists create art by eye, all the textures" values are in sRGB space so if we use those textures as they are in our rendering application we have to take this into account. Before we knew about gamma correction this wasn"t really an issue, because the textures looked good in sRGB space which is the same space we worked in; the textures were displayed exactly as they are which was fine. However, now that we"re displaying everything in linear space, the texture colors will be off as the following image shows:

The texture image is way too bright and this happens because it is actually gamma corrected twice! Think about it, when we create an image based on what we see on the monitor, we effectively gamma correct the color values of an image so that it looks right on the monitor. Because we then again gamma correct in the renderer, the image ends up way too bright.

The other solution is to re-correct or transform these sRGB textures to linear space before doing any calculations on their color values. We can do this as follows:

To do this for each texture in sRGB space is quite troublesome though. Luckily OpenGL gives us yet another solution to our problems by giving us the GL_SRGB and GL_SRGB_ALPHA internal texture formats.

If we create a texture in OpenGL with any of these two sRGB texture formats, OpenGL will automatically correct the colors to linear-space as soon as we use them, allowing us to properly work in linear space. We can specify a texture as an sRGB texture as follows:

You should be careful when specifying your textures in sRGB space as not all textures will actually be in sRGB space. Textures used for coloring objects (like diffuse textures) are almost always in sRGB space. Textures used for retrieving lighting parameters (like specular maps and normal maps) are almost always in linear space, so if you were to configure these as sRGB textures the lighting will look odd. Be careful in which textures you specify as sRGB.

With our diffuse textures specified as sRGB textures you get the visual output you"d expect again, but this time everything is gamma corrected only once.

Something else that"s different with gamma correction is lighting attenuation. In the real physical world, lighting attenuates closely inversely proportional to the squared distance from a light source. In normal English it simply means that the light strength is reduced over the distance to the light source squared, like below:

However, when using this equation the attenuation effect is usually way too strong, giving lights a small radius that doesn"t look physically right. For that reason other attenuation functions were used (like we discussed in the basic lighting chapter) that give much more control, or the linear equivalent is used:

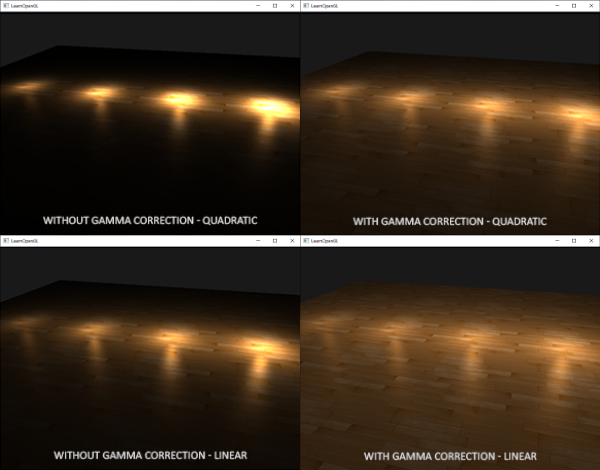
The linear equivalent gives more plausible results compared to its quadratic variant without gamma correction, but when we enable gamma correction the linear attenuation looks too weak and the physically correct quadratic attenuation suddenly gives the better results. The image below shows the differences:

The cause of this difference is that light attenuation functions change brightness, and as we weren"t visualizing our scene in linear space we chose the attenuation functions that looked best on our monitor, but weren"t physically correct. Think of the squared attenuation function: if we were to use this function without gamma correction, the attenuation function effectively becomes: \((1.0 / distance^2)^{2.2}\) when displayed on a monitor. This creates a much larger attenuation from what we originally anticipated. This also explains why the linear equivalent makes much more sense without gamma correction as this effectively becomes \((1.0 / distance)^{2.2} = 1.0 / distance^{2.2}\) which resembles its physical equivalent a lot more.

The more advanced attenuation function we discussed in the basic lighting chapter still has its place in gamma corrected scenes as it gives more control over the exact attenuation (but of course requires different parameters in a gamma corrected scene).

You can find the source code of this simple demo scene here. By pressing the spacebar we switch between a gamma corrected and un-corrected scene with both scenes using their texture and attenuation equivalents. It"s not the most impressive demo, but it does show how to actually apply all techniques.

To summarize, gamma correction allows us to do all our shader/lighting calculations in linear space. Because linear space makes sense in the physical world, most physical equations now actually give good results (like real light attenuation). The more advanced your lighting becomes, the easier it is to get good looking (and realistic) results with gamma correction. That is also why it"s advised to only really tweak your lighting parameters as soon as you have gamma correction in place.

Your monitor’s gamma tells you its pixels’ luminance at every brightness level, from 0-100%. Lower gamma makes shadows looks brighter and can result in a flatter, washed out image, where it"s harder to see brighter highlights. Higher gamma can make it harder to see details in shadows. Some monitors offer different gamma modes, allowing you to tweak image quality to your preference. The standard for the sRGBcolor space, however, is a value of 2.2.

Gamma is important because it affects the appearance of dark areas, like blacks and shadows and midtones, as well as highlights. Monitors with poor gamma can either crush detail at various points or wash it out, making the entire picture appear flat and dull. Proper gamma leads to more depth and realism and a more three-dimensional image.

The image gallery below (courtesy of BenQ(opens in new tab)) shows an image with the 2.2 gamma standard compared to that same image with low gamma and with high gamma.

Typically, if you are running on the Windows operating system, the most accurate color is achieved with a gamma value of 2.2 (for Mac OS, the ideal gamma value is 1.8). So when testing monitors, we strive for a gamma value of 2.2. A monitor’s range of gamma values indicates how far the lowest and highest values differ from the 2.2 standard (the smaller the difference, the better).

In our monitor reviews, we’ll show you gamma charts like the one above, with the x axis representing different brightness levels. The yellow line represents 2.2 gamma value. The closer the gray line conforms to the yellow line, the better.

The Levels center slider is a multiplier of the current image gamma. I don"t find that "multiplier" written about so much any more, but it was popular, widely known and discussed 15-20 years ago (CRT days, back when we knew what gamma was). Gamma used to be very important, but today, we still encode with 1/2.2, and the LCD monitor must decode with 2.2, and for an LCD monitor, gamma is just an automatic no-op now (printers and CRT still make use of it).

Evidence of the tool as multiplier: An eyedropper on the gray road at the curve ahead in the middle image at gamma 2.2 reads 185 (I"m looking at the red value). Gamma 2.2 puts that linear value at 126 (midscale). 126 at gamma 1 is 126 (measured in top image, 0.45x x 2.2 = gamma 1). 126 at gamma 4.8 is 220 (measured in bottom image, 2.2x x 2.2 = gamma 4.8). Q.E.D.

Today, our LCD display is considered linear and technically does not need gamma. However we still necessarily continue gamma to provide compatibility with all the world"s previous images and video systems, and for CRT and printers too. The LCD display simply uses a chip (LookUp table, next page) to decode it first (discarding gamma correction to necessarily restore the original linear image). Note that gamma is a Greek letter used for many variables in science (like X is used in algebra, used many ways), so there are also several other unrelated uses of the word gamma, in math and physics, or for film contrast, etc, but all are different unrelated concepts. For digital images, the use of the term gamma is to describe the CRT response curve.

We must digitize an image first to show it on our computer video system. But all digital cameras and scanners always automatically add gamma to all tonal images. By "tonal", I mean a color or grayscale image is tonal (has many different tones), as opposed to a one-bit line art image (two colors, black or white, 0 or 1, which has no gray tones, like clip art or fax) does not need or get gamma (values 0 and 1 are entirely unaffected by gamma).

Gamma correction is automatically done to any image from by any digital camera (still or movie), and from any scanner, or created in graphic editors... any digital tonal image that might be created in any way. A raw image is an exception, only because then gamma is deferred until later when it actually becomes a RGB image. Gamma is an invisible background process, and we don"t have to necessarily be aware of it, it just always happens. This does mean that all of our image histograms contain and show gamma data. The 128 value that we may think of as midscale is not middle tone of the histograms we see. This original linear 128 middle value (middle at 50% linear data, 1 stop down from 255) is up at about 186 in gamma data, and in our histograms.

The reason we use gamma correction. For many years, CRT was the only video display we had (other than projecting film). But CRT is not linear, and requires heroic efforts to properly use them for tonal images (photos and TV). The technical reason we needed gamma is that the CRT light beam intensity efficiency varies with the tubes electron gun signal voltage. CRT does not use the decode formula, which simply resulted from the study of what the non-linear CRT losses already actually do in the act of showing it on a CRT ... the same effect. The non-linear CRT simply shows the tones, with the response is sort of as if the numeric values were squared first (2.2 is near 2). These losses have variable results, depending on the tones value, but the brighter values are brighter, and the darker values are darker. Not linear.

How does CRT Gamma Correction actually do its work? Gamma 2.2 is roughly 2, so there"s only a small difference from 1/2 square root, and 2 squared. I hope that approximation simplifies instead of confusing. So Encoding Gamma Correction input to the power of 1/2.2 is roughly the square root, which condenses the image gamma data range smaller. Then later, CRT Gamma Decodes it to power of 2.2, roughly squared, which expands it to bring it back exactly to the original value (reversible). Specifically, for a numerical example for two tones 225 and 25, value 225 is 9x brighter then 25 (225/25=9). But (using easier exponent 2 instead of 2.2), the square roots are 15 and 5, which is only 3 times more then, compressed together, much less difference ... 3² is 9 (and if we use 2.2, then 2.7 times more). So in that way, gamma correction data boosts the low values higher, they move up more near the bright values. And 78% of the encoded values end up above the 127 50% midpoint (see LUT on next page, or see curve above). So to speak, the file data simply stores roughly the square root, and then the CRT decodes by showing it roughly squared, for no net change then, which was the plan, to reproduce the original linear data. The reason is because the CRT losses are going to show it squared regardless (but specifically, the CRT response result is power of 2.2).

Not to worry, our eye is NEVER EVER going to see any of these gamma values. Because, then the non-linear CRT gamma output is a roughly squared response to expand it back (restored to our first 225 and 25 linear values by the actual CRT losses that we planned for). CRT losses still greatly reduce the low values, but which were first boosted in preparation for it. So this gamma correction operation can properly show the dim values linearly again (since dim starts off condensed, up much closer to the strong values, and then becomes properly dim when expanded by CRT losses.) It has worked great for many years. But absolutely nothing about gamma is related to the human eye response. We don"t need to even care how the eye works. The eye NEVER sees any gamma data. The eye merely looks at the final linear reproduction of our image on the screen, after it is all over. The eye only wants to see an accurate linear reproduction of the original scene. How hard is that?

Then more recently, we invented LCD displays which became very popular. These were considered linear devices, so technically, they didn"t need CRT gamma anymore. But if we did create and use gamma-free devices, then our device couldn"t show any of the world"s gamma images properly, and the world could not show our images properly. And our gamma-free images would be incompatible with CRT too. There"s no advantage of that, so we"re locked into gamma, and for full compatibility, we simply just continue encoding our images with gamma like always before. This is easy to do today, it just means the LCD device simply includes a little chip to first decode gamma and then show the original linear result. Perhaps it is a slight wasted effort, but it"s easy, and reversible, and the compatibility reward is huge (because all the worlds images are gamma encoded). So no big deal, no problem, it works great. Again, the eye never sees any gamma data, it is necessarily decoded first back to the linear original. We may not even realize gamma is a factor in our images, but it always is. Our histograms do show the numerical gamma data values, but the eye never sees a gamma image. Never ever.

Printers and Macintosh: Our printers naturally expect to receive gamma images too (because that"s all that exists). Publishing and printer devices do also need some of gamma, not as much as 2.2 for the CRT, but the screening methods need most of it (for dot gain, which is when the ink soaks in to the paper and spreads wider). Until recently (2009), Apple Mac computers used gamma 1.8 images. They could use the same CRT monitors as Windows computers, and those monitors obviously were gamma 2.2, but Apple split this up. This 1.8 value was designed for the early laser printers that Apple manufactured then (and for publishing prepress), to be what the printer needed. Then the Mac video hardware added another 0.4 gamma correction for the CRT monitor, so the video result was an unspoken gamma 2.2, roughly — even if their files were gamma 1.8. That worked before internet, before images were shared widely. But now, the last few Mac versions (since OS 10.6) now observe the sRGB world standard gamma 2.2 in the file, because all the world"s images are already encoded that way, and we indiscriminately share them via the internet now. Compatibility is a huge deal, because all the worlds grayscale and color photo images are tonal images. All tonal images are gamma encoded. But yes, printers are also programmed to deal with the gamma 2.2 data they receive, and know to adjust it to their actual needs.

Extremely few PC computers could even show images before 1987. An early wide-spread source of images was Compuserve"s GIF file in 1987 (indexed color, an 8 bit index into a palette of 256 colors maximum, concerned with small file size and dialup modem speeds instead of image quality). Better for graphics, and indexed color is still good for most simple graphics (with not very many colors). GIF wasn"t great for color photos, but at the time, some of these did seem awesome seen on the CRT monitor. Then 8-bit JPG and TIF files (16.7 million possible colors) were developed a few years later, and 24-bit video cards (for 8-bit RGB color instead of indexed color) became the norm soon, and the internet came too, and in just a few years, use of breathtaking computer photos literally exploded to be seen everywhere. Our current 8 bits IS THE SOLUTION chosen to solve the problem, and it has been adequate for 30+ years. Specifically, the definitions are that these 8-bit files had three 8-bit RGB channels for 24 bit color, for RGB 256x256x256 = 16.7 million possible colors.

While we"re on history, this CRT problem (non-linear response curve named gamma) was solved by earliest television (first NTSC spec in 1941). Without this "gamma correction", the CRT screen images came out unacceptably dark. Television broadcast stations intentionally boosted the dark values (with gamma correction, encoded to be opposite to the expected CRT losses, that curve called gamma). That was vastly less expensive in vacuum tube days than building gamma circuitry into every TV set. Today, it"s just a very simple chip for the LCD monitors that don"t need gamma... LCD simply decodes it to remove gamma now, to restore it to linear.

This is certainly NOT saying gamma does not matter now. We still do gamma for compatibility (for CRT, and to see all of the worlds images, and so all the worlds systems can view our images). The LCD monitors simply know to decode and remove gamma 2.2, and for important compatibility, you do need to provide them with a proper gamma 2.2 to process, because 2.2 is what they will remove. sRGB profile is the standard way to do that. This is very easy, and mostly fully automatic, about impossible to bypass.

The 8-bit issue is NOT that 8-bit gamma data can only store integers in range of [0..255]. Meaning, we could use the same 8-bit gamma file for a 12 bit or 16 bit display device (if there were any). The only 8-bit issue is that our display devices can only show 8 bit data. See this math displayed on next page.

Unfortunately, some do like to imagine that gamma must still be needed (now for the eye?), merely because they once read Poynton that the low end steps in gamma data better matches the human eye 1% steps of perception. Possibly it may, but it was explained as coincidental. THIS COULD NOT MATTER LESS. They"re simply wrong about the need of the eye, it is false rationalization, obviously not realizing that our eye Never sees any gamma data. Never ever. We know to encode gamma correction of exponent 1/2.2 for CRT, which is needed because we"ve learned the lossy CRT response will do the opposite. It really wouldn"t matter which math operation we use for the linear LCD, if any, so long as the LCD still knows to do the exact opposite, to reverse it back out. But the LCD monitor necessarily does expect gamma 2.2 data anyway, and gamma 2.2 is exactly undone. Gamma data is universally present in existing images, and it is always first reversibly decoded back to be the original linear reproduction that our eye needs to view. That"s the goal, linear is exactly what our eye expects. Our e