wave and particle behaviors of lcd displays free sample

The theoretical sketch of the wave-particle scheme for the single photon is displayed in Fig. 1. A photon is initially prepared in a polarization state \(\left| {{\psi _0}} \right\rangle = {\rm{cos}}\,\alpha \left| {\rm V} \right\rangle + {\rm{sin}}\,\alpha \left| {\rm{H}} \right\rangle\), where \(\left| {\rm V} \right\rangle\) and \(\left| {\rm{H}} \right\rangle\) are the vertical and horizontal polarization states and α is adjustable by a preparation half-wave plate (not shown in the figure). After crossing the preparation part of the setup of Fig. 1 (see Supplementary Notes 1 and 2 and Supplementary Fig. 1 for details), the photon state is

$$\left| {{\psi _{\rm{f}}}} \right\rangle = {\rm{cos}}\,\alpha \left| {{\rm{wave}}} \right\rangle + {\rm{sin}}\,\alpha \left| {{\rm{particle}}} \right\rangle ,$$

$$\begin{array}{*{20}{l}}\\ {\left| {{\rm{wave}}} \right\rangle } = {{e^{i{\phi _1}/2}}\left( {{\rm{cos}}\frac{{{\phi _1}}}{2}\left| 1 \right\rangle - i\,{\rm{sin}}\frac{{{\phi _1}}}{2}\left| 3 \right\rangle } \right),} \hfill \\ {\left| {{\rm{particle}}} \right\rangle } = {\frac{1}{{\sqrt 2 }}\left( {\left| 2 \right\rangle + {e^{i{\phi _2}}}\left| 4 \right\rangle } \right),} \hfill \\ \end{array}$$

operationally represent the capacity \(\left( {\left| {{\rm{wave}}} \right\rangle } \right)\) and incapacity \(\left( {\left| {{\rm{particle}}} \right\rangle } \right)\) of the photon to produce interference\(\left| {{\rm{wave}}} \right\rangle\) state the probability of detecting the photon in the path \(\left| n \right\rangle \,\) (n = 1, 3) depends on the phase ϕ

1: the photon must have traveled along both paths simultaneously (see upper MZI in Fig. 1), revealing its wave behavior. Instead, for the \(\left| {{\rm{particle}}} \right\rangle\) state the probability to detect the photon in the path \(\left| n \right\rangle \,\) (n = 2, 4) is 1/2, regardless of phase ϕ

2: thus, the photon must have crossed only one of the two paths (see lower MZI of Fig. 1), showing its particle behavior. Notice that the scheme is designed in such a way that \(\left| {\rm V} \right\rangle\)

Conceptual figure of the wave-particle toolbox. A single photon is coherently separated in two spatial modes by means of a polarizing beam-splitter (PBS) according to its initial polarization state (in). A half-wave plate (HWP) is placed after the PBS to obtain equal polarizations between the two modes. One mode is injected in a complete Mach-Zehnder interferometer (MZI) with phase ϕ

1, thus exhibiting wave-like behavior. The second mode is injected in a Mach-Zehnder interferometer lacking the second beam-splitter, thus exhibiting particle-like behavior (no dependence on ϕ

To verify the coherent wave-particle superposition as a function of the parameter α, the wave and particle states have to interfere at the detection level. This goal is achieved by exploiting two symmetric beam-splitters where the output paths (modes) are recombined, as illustrated in the detection part of Fig. 1. The probability P

We remark that the terms \({{\cal I}_{\rm{c}}}\), \({{\cal I}_{\rm{s}}}\) in the detection probabilities exclusively stem from the interference between the \(\left| {{\rm{wave}}} \right\rangle\) and \(\left| {{\rm{particle}}} \right\rangle\) components appearing in the generated superposition state \(\left| {{\psi _{\rm{f}}}} \right\rangle\) of Eq. (1). This fact is further evidenced by the appearance, in these interference terms, of the factor \({\cal C} = {\rm{sin}}\,2\alpha\), which is the amount of quantum coherence owned by \(\left| {{\psi _{\rm{f}}}} \right\rangle\) in the basis {\(\left| {{\rm{wave}}} \right\rangle\), \(\left| {{\rm{particle}}} \right\rangle\)} theoretically quantified according to the standard l

1-norm\({{\cal I}_{\rm{c}}}\), \({{\cal I}_{\rm{s}}}\) are always identically zero (independently of phase values) when the final state of the photon is: (i) \(\left| {{\rm{wave}}} \right\rangle\) (α = 0); (ii) \(\left| {{\rm{particle}}} \right\rangle\) (α = π/2); (iii) a classical incoherent mixture \({\rho _{\rm{f}}} = {\rm{co}}{{\rm{s}}^2}\alpha \left| {{\rm{wave}}} \right\rangle \left\langle {{\rm{wave}}} \right| + {\rm{si}}{{\rm{n}}^2}\alpha \left| {{\rm{particle}}} \right\rangle \left\langle {{\rm{particle}}} \right|\) (which can be theoretically produced by the same scheme starting from an initial mixed polarization state of the photon).

The experimental single-photon toolbox, realizing the proposed scheme of Fig. 1, is displayed in Fig. 2 (see Methods for more details). The implemented layout presents the advantage of being interferometrically stable, thus not requiring active phase stabilization between the modes. Figure 3 shows the experimental results for the measured single-photon probabilities P

n. For α = 0, the photon is vertically polarized and entirely reflected from the PBS to travel along path 1, then split at BS1 into two paths, both leading to the same BS3 which allows these two paths to interfere with each other before detection. The photon detection probability at each detector Dn (n = 1, 2, 3, 4) depends on the phase shift ϕ

1: \({P_1}\left( {\alpha = 0} \right) = {P_2}\left( {\alpha = 0} \right) = \frac{1}{2}{\rm{co}}{{\rm{s}}^2}\frac{{{\phi _1}}}{2}\), \({P_3}\left( {\alpha = 0} \right) = {P_4}\left( {\alpha = 0} \right) = \frac{1}{2}{\rm{si}}{{\rm{n}}^2}\frac{{{\phi _1}}}{2}\), as expected from Eqs. (3) and (4). After many such runs an interference pattern emerges, exhibiting the wave-like nature of the photon. Differently, if initially α = π/2, the photon is horizontally polarized and, as a whole, transmitted by the PBS to path 2, then split at BS2 into two paths (leading, respectively, to BS4 and BS5) which do not interfere anywhere. Hence, the phase shift ϕ

2 plays no role on the photon detection probability and each detector has an equal chance to click: \({P_1}\left( {\alpha = \frac{\pi }{2}} \right) = {P_2}\left( {\alpha = \frac{\pi }{2}} \right) = {P_3}\left( {\alpha = \frac{\pi }{2}} \right) = {P_4}\left( {\alpha = \frac{\pi }{2}} \right) = \frac{1}{4}\), as predicted by Eqs. (3) and (4), showing particle-like behavior without any interference pattern. Interestingly, for 0 < α < π/2, the photon simultaneously behaves like wave and particle. The coherent continuous morphing transition from wave to particle behavior as α varies from 0 to π/2 is clearly seen from Fig. 4a and contrasted with the morphing observed for a mixed incoherent wave-particle state ρ

2 = 0, the coherence of the generated state is also directly quantified by measuring the expectation value of an observable \(\sigma _x^{1234}\), defined in the four-dimensional basis of the photon paths \(\left\{ {\left| 1 \right\rangle ,\left| 2 \right\rangle ,\left| 3 \right\rangle ,\left| 4 \right\rangle } \right\}\) of the preparation part of the setup as a Pauli matrix σ

x between modes (1, 2) and between modes (3, 4). It is then possible to straightforwardly show that \(\left\langle {\sigma _x^{1234}} \right\rangle = {\rm{Tr}}\left( {\sigma _x^{1234}{\rho _{\rm{f}}}} \right) = 0\) for any incoherent state ρ

f, while \(\sqrt 2 \left\langle {\sigma _x^{1234}} \right\rangle = {\rm{sin}}\,2\alpha = {\cal C}\) for an arbitrary state of the form \(\left| {{\psi _{\rm{f}}}} \right\rangle\) defined in Eq. (1). Insertion of beam-splitters BS4 and BS5 in the detection part of the setup (corresponding to β = 22.5° in the output wave-plate of Fig. 2) rotates the initial basis \(\left\{ {\left| 1 \right\rangle ,\left| 2 \right\rangle ,\left| 3 \right\rangle ,\left| 4 \right\rangle } \right\}\) generating a measurement basis of eigenstates of \(\sigma _x^{1234}\), whose expectation value is thus obtained in terms of the detection probabilities as \(\left\langle {\sigma _x^{1234}} \right\rangle = {P_1} - {P_2} + {P_3} - {P_4}\) (see Supplementary Note 2). As shown in Fig. 4c, d, the observed behavior of \(\sqrt 2 \left\langle {\sigma _x^{1234}} \right\rangle\) as a function of α confirms the theoretical predictions for both coherent \(\left| {{\psi _{\rm{f}}}} \right\rangle\) (Fig. 4c) and mixed (incoherent) ρ

f wave-particle states (the latter being obtained in the experiment by adding a relative time delay in the interferometer paths larger than the photon coherence time to lose quantum interference, Fig. 4d).

Experimental setup for wave-particle states. a Overview of the apparatus for the generation of single-photon wave-particle superposition. An heralded single-photon is prepared in an arbitrary linear polarization state through a half-wave plate rotated at an angle α/2 and injected into the wave-particle toolbox. b Overview of the apparatus for the generation of a two-photon wave-particle entangled state. Each photon of a polarization entangled state is injected into an independent wave-particle toolbox to prepare the output state. c Actual implemented wave-particle toolbox, reproducing the action of the scheme shown in Fig. 1. Top subpanel: top view of the scheme, where red and purple lines represent optical paths lying in two vertical planes. Bottom subpanel: 3-d scheme of the apparatus. The interferometer is composed of beam-displacing prisms (BDP), half-wave plates (HWP), and liquid crystal devices (LC), the latter changing the phases ϕ

2. The output modes are finally separated by means of a polarizing beam-splitter (PBS). The scheme corresponds to the presence of BS4 and BS5 in Fig. 1 for β = 22.5°, while setting β = 0 equals to the absence of BS4 and BS5. The same color code for the optical elements (reported in the figure legend) is employed for the top view and for the 3-d view of the apparatus. d Picture of the experimental apparatus. The green frame highlights the wave-particle toolbox

1, for different values of α. a Wave behavior (α = 0). b Particle behavior (α = π/2). c Coherent wave-particle superposition (α = π/4). d Incoherent mixture of wave and particle behaviors (α = π/4). Points: experimental data. Dashed curves: best-fit of the experimental data. Color legend: orange (P1), green (P2), purple (P3), blue (P

1 and of the angle α. Points: experimental data. Surfaces: theoretical expectations. In all plots, error bars are standard deviation due to the Poissonian statistics of single-photon counting

4). In a black triangles highlighted the position for wave behavior (α = 0), black circle for particle behavior (α = π/2) and black diamonds highlight the position for coherent wave-particle superposition behavior (α = π/4). c Coherence measure \(\sqrt 2 \left\langle {\sigma _x^{1234}} \right\rangle\) as a function of α in the coherent case and d for an incoherent mixture (the latter showing no dependence on α). Points: experimental data. Solid curves: theoretical expectations. Error bars are standard deviations due to the Poissonian statistics of single-photon counting

The above single-photon scheme constitutes the basic toolbox which can be extended to create a wave-particle entangled state of two photons, as shown in Fig. 2b. Initially, a two-photon polarization maximally entangled state \({\left| \Psi \right\rangle _{{\rm{AB}}}} = \frac{1}{{\sqrt 2 }}\left( {\left| {{\rm VV}} \right\rangle + \left| {{\rm{HH}}} \right\rangle } \right)\) is prepared (the procedure works in general for arbitrary weights, see Supplementary Note 3). Each photon is then sent to one of two identical wave-particle toolboxes which provide the final state

$${\left| \Phi \right\rangle _{{\rm{AB}}}} = \frac{1}{{\sqrt 2 }}\left( {\left| {{\rm{wave}}} \right\rangle \left| {{\rm{wave}"}} \right\rangle + \left| {{\rm{particle}}} \right\rangle \left| {{\rm{particle}"}} \right\rangle } \right),$$

where the single-photon states \(\left| {{\rm{wave}}} \right\rangle\), \(\left| {{\rm{particle}}} \right\rangle\), \(\left| {{\rm{wave}"}} \right\rangle\), \(\left| {{\rm{particle}"}} \right\rangle\) are defined in Eq. (2), with parameters and paths related to the corresponding wave-particle toolbox. Using the standard concurrenceC to quantify the amount of entanglement of this state in the two-photon wave-particle basis, one immediately finds C = 1. The generated state \({\left| \Phi \right\rangle _{{\rm{AB}}}}\) is thus a wave-particle maximally entangled state (Bell state) of two photons in separated locations.

The output two-photon state is measured after the two toolboxes. The results are shown in Fig. 5. Coincidences between the four outputs of each toolbox are measured by varying ϕ

1 and \(\phi _1^{\prime}\). The first set of measurements (Fig. 5a–d) is performed by setting the angles of the output wave-plates (see Fig. 2c) at {β = 0, β′ = 0}, corresponding to removing both BS4 and BS5 in Fig. 1 (absence of interference between single-photon wave and particle states). In this case, detectors placed at outputs (1, 3) and (1′, 3′) reveal wave-like behavior, while detectors placed at outputs (2, 4) and (2′, 4′) evidence a particle-like one. As expected, the two-photon probabilities \({P_{n{n^{\prime}}}}\) for the particle detectors remain unchanged while varying ϕ

1 and \(\phi _1^{\prime}\), whereas the \({P_{nn"}}\) for the wave detectors show interference fringes. Moreover, no contribution of crossed wave-particle coincidences \({P_{nn"}}\) is obtained, due to the form of the entangled state. The second set of measurements (Fig. 5e–h) is performed by setting the angles of the output wave-plates at {β = 22.5°, β′ = 22.5°}, corresponding to the presence of BS4 and BS5 in Fig. 1 (the presence of interference between single-photon wave and particle states). We now observe nonzero contributions across all the probabilities depending on the specific settings of phases ϕ

1 and \(\phi _1^{\prime}\). The presence of entanglement in the wave-particle behavior is also assessed by measuring the quantity \({\cal E} = {P_{22"}} - {P_{21"}}\) as a function of ϕ

1, with fixed \(\phi _1^{\prime} = {\phi _2} = \phi _2^{\prime} = 0\). According to the general expressions of the coincidence probabilities (see Supplementary Note 3), \({\cal E}\) is proportional to the concurrence C and identically zero (independently of phase values) if and only if the wave-particle two-photon state is separable (e.g., \(\left| {{\rm{wave}}} \right\rangle\) ⊗ \(\left| {{\rm{wave}"}} \right\rangle\) or a maximal mixture of two-photon wave and particle states). For \(\left| \Phi \right\rangle\)

AB of Eq. (5) the theoretical prediction is \({\cal E} = \left( {1{\rm{/}}4} \right){\rm{co}}{{\rm{s}}^{\rm{2}}}\left( {{\phi _1}{\rm{/}}2} \right)\), which is confirmed by the results reported in Fig. 5i, j (within the reduction due to visibility). A further test of the generated wave-particle entanglement is finally performed by the direct measure of the expectation values \(\left\langle {\cal W} \right\rangle = {\rm{Tr}}\left( {{\cal W}\rho } \right)\) of a suitable entanglement witness

z Pauli matrix between modes (1, 2) and between modes (3, 4). The measurement basis of \(\sigma _z^{1234}\) is that of the initial paths \(\left\{ {\left| 1 \right\rangle ,\left| 2 \right\rangle ,\left| 3 \right\rangle ,\left| 4 \right\rangle } \right\}\) exiting the preparation part of the single-photon toolbox. It is possible to show that \({\rm{Tr}}\left( {{\cal W}{\rho _{\rm{s}}}} \right) \ge 0\) for any two-photon separable state ρ

e is entangled in the photons wave-particle behavior (see Supplementary Note 3). The expectation values of \({\cal W}\) measured in the experiment in terms of the 16 coincidence probabilities P

1 = 0, \(\phi _1^\prime\) = π). These observations altogether prove the existence of quantum correlations between wave and particle states of two photons in the entangled state \(\left| \Phi \right\rangle\)

Generation of wave-particle entangled superposition with a two-photon state. Measurements of the output coincidence probabilities \({P_{nn"}}\) to detect one photon in output mode n of the first toolbox and one in the output mode n′ of the second toolbox, with different phases ϕ

1 = π and \(\phi _1^{\prime} = \pi\). White bars: theoretical predictions. Colored bars: experimental data. Orange bars: \({P_{n{n^{\prime}}}}\) contributions for detectors Dn and \({{\rm{D}}_{n"}}\) linked to wave-like behavior for both photons (in the absence of BS4 and BS5). Cyan bars: \({P_{nn"}}\) contributions for detectors Dn and \({{\rm{D}}_{n"}}\) linked to particle-like behavior for both photons (in the absence of BS4 and BS5). Magenta bars: \({P_{nn"}}\) contributions for detectors Dn and \({{\rm{D}}_{n"}}\) linked to wave-like behavior for one photon and particle-like behavior for the other one (in absence of BS4 and BS5). Darker regions in colored bars correspond to 1 σ error interval, due to the Poissonian statistics of two-photon coincidences. i, j, Quantitative verification of wave-particle entanglement. i, \({P_{22"}}\) (blue) and \({P_{21"}}\) (green) and j, \({\cal E} = {P_{22"}} - {P_{21"}}\), as a function of ϕ

1 for \(\phi _1^{\prime} = 0\) and {β = 22.5°, β′ = 22.5°}. Error bars are standard deviations due to the Poissonian statistics of two-photon coincidences. Dashed curves: best-fit of the experimental data

This section contains lecture notes in both PDF and PowerPoint formats. Some of the slides include animations, which can be seen by viewing the PowerPoint file as a slide show.

A photoelectron with a kinetic energy of 5.0eV is emitted from a copper plate. Determine the frequency in Hertz for the light that impacted the plate.

Liquid crystal (LC) is a state of matter whose properties are between those of conventional liquids and those of solid crystals. For example, a liquid crystal may flow like a liquid, but its molecules may be oriented in a crystal-like way. There are many types of LC phases, which can be distinguished by their optical properties (such as textures). The contrasting textures arise due to molecules within one area of material ("domain") being oriented in the same direction but different areas having different orientations. LC materials may not always be in a LC state of matter (just as water may be ice or water vapor).

Thermotropic and lyotropic liquid crystals consist mostly of organic molecules, although a few minerals are also known. Thermotropic LCs exhibit a phase transition into the LC phase as temperature changes. Lyotropic LCs exhibit phase transitions as a function of both temperature and concentration of molecules in a solvent (typically water). Metallotropic LCs are composed of both organic and inorganic molecules; their LC transition additionally depends on the inorganic-organic composition ratio.

Examples of LCs exist both in the natural world and in technological applications. Lyotropic LCs abound in living systems; many proteins and cell membranes are LCs, as well as the tobacco mosaic virus. LCs in the mineral world include solutions of soap and various related detergents, and some clays. Widespread liquid-crystal displays (LCD) use liquid crystals.

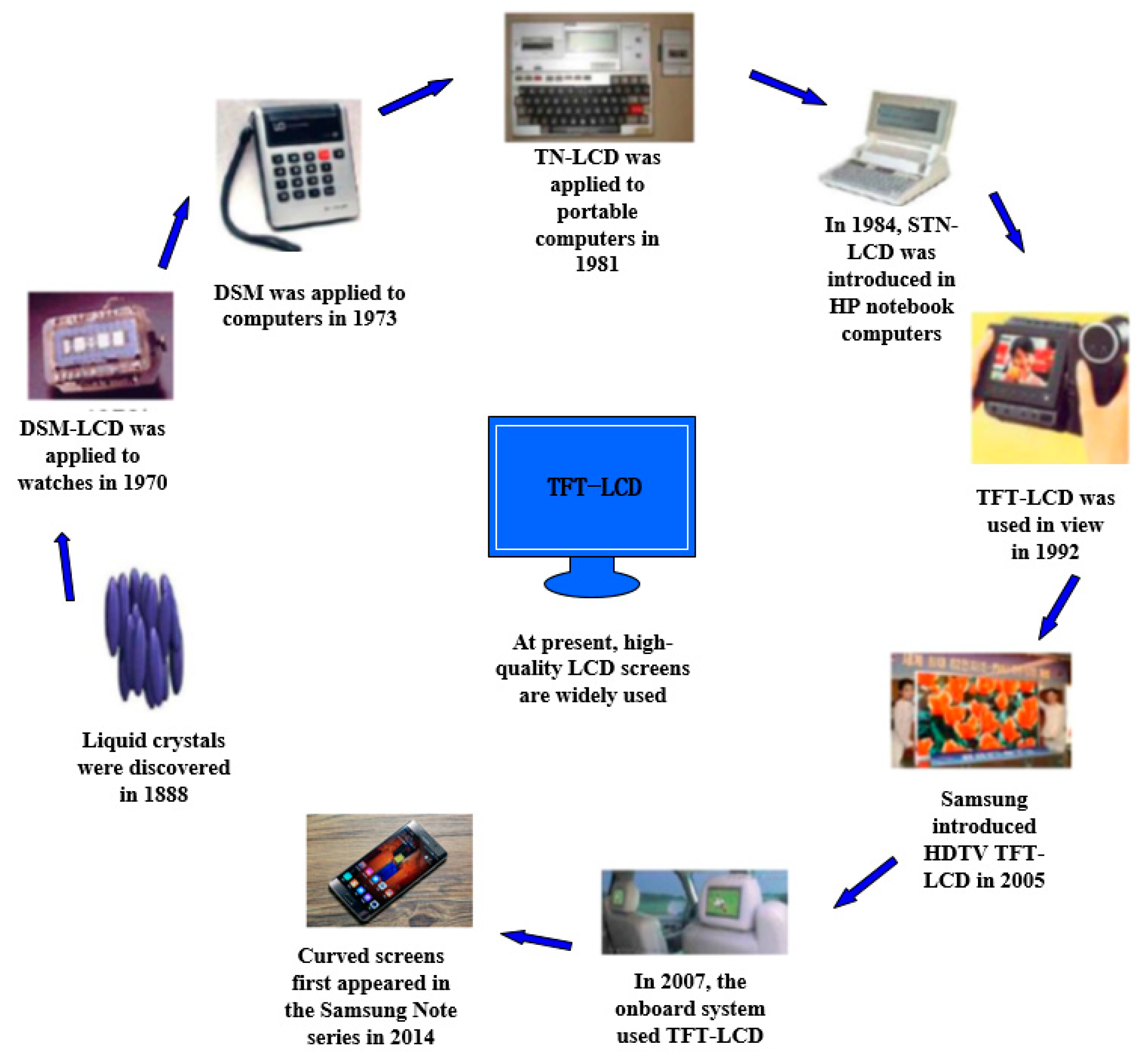
In 1888, Austrian botanical physiologist Friedrich Reinitzer, working at the Karl-Ferdinands-Universität, examined the physico-chemical properties of various derivatives of cholesterol which now belong to the class of materials known as cholesteric liquid crystals. Previously, other researchers had observed distinct color effects when cooling cholesterol derivatives just above the freezing point, but had not associated it with a new phenomenon. Reinitzer perceived that color changes in a derivative cholesteryl benzoate were not the most peculiar feature.

He found that cholesteryl benzoate does not melt in the same manner as other compounds, but has two melting points. At 145.5 °C (293.9 °F) it melts into a cloudy liquid, and at 178.5 °C (353.3 °F) it melts again and the cloudy liquid becomes clear. The phenomenon is reversible. Seeking help from a physicist, on March 14, 1888, he wrote to Otto Lehmann, at that time a Aachen. They exchanged letters and samples. Lehmann examined the intermediate cloudy fluid, and reported seeing crystallites. Reinitzer"s Viennese colleague von Zepharovich also indicated that the intermediate "fluid" was crystalline. The exchange of letters with Lehmann ended on April 24, with many questions unanswered. Reinitzer presented his results, with credits to Lehmann and von Zepharovich, at a meeting of the Vienna Chemical Society on May 3, 1888.

By that time, Reinitzer had discovered and described three important features of cholesteric liquid crystals (the name coined by Otto Lehmann in 1904): the existence of two melting points, the reflection of circularly polarized light, and the ability to rotate the polarization direction of light.

After his accidental discovery, Reinitzer did not pursue studying liquid crystals further. The research was continued by Lehmann, who realized that he had encountered a new phenomenon and was in a position to investigate it: In his postdoctoral years he had acquired expertise in crystallography and microscopy. Lehmann started a systematic study, first of cholesteryl benzoate, and then of related compounds which exhibited the double-melting phenomenon. He was able to make observations in polarized light, and his microscope was equipped with a hot stage (sample holder equipped with a heater) enabling high temperature observations. The intermediate cloudy phase clearly sustained flow, but other features, particularly the signature under a microscope, convinced Lehmann that he was dealing with a solid. By the end of August 1889 he had published his results in the Zeitschrift für Physikalische Chemie.

Lehmann"s work was continued and significantly expanded by the German chemist Daniel Vorländer, who from the beginning of the 20th century until he retired in 1935, had synthesized most of the liquid crystals known. However, liquid crystals were not popular among scientists and the material remained a pure scientific curiosity for about 80 years.

After World War II, work on the synthesis of liquid crystals was restarted at university research laboratories in Europe. George William Gray, a prominent researcher of liquid crystals, began investigating these materials in England in the late 1940s. His group synthesized many new materials that exhibited the liquid crystalline state and developed a better understanding of how to design molecules that exhibit the state. His book Molecular Structure and the Properties of Liquid CrystalsUniversity of Cincinnati and later at Kent State University. In 1965, he organized the first international conference on liquid crystals, in Kent, Ohio, with about 100 of the world"s top liquid crystal scientists in attendance. This conference marked the beginning of a worldwide effort to perform research in this field, which soon led to the development of practical applications for these unique materials.

Liquid crystal materials became a focus of research in the development of flat panel electronic displays beginning in 1962 at RCA Laboratories.nematic liquid crystal at 125 °C, he observed the formation of a regular pattern that he called domains (now known as Williams Domains). This led his colleague George H. Heilmeier to perform research on a liquid crystal-based flat panel display to replace the cathode ray vacuum tube used in televisions. But the para-azoxyanisole that Williams and Heilmeier used exhibits the nematic liquid crystal state only above 116 °C, which made it impractical to use in a commercial display product. A material that could be operated at room temperature was clearly needed.

In 1966, Joel E. Goldmacher and Joseph A. Castellano, research chemists in Heilmeier group at RCA, discovered that mixtures made exclusively of nematic compounds that differed only in the number of carbon atoms in the terminal side chains could yield room-temperature nematic liquid crystals. A ternary mixture of Schiff base compounds resulted in a material that had a nematic range of 22–105 °C.operating temperature range eventually became the industry standard and is still used to tailor materials to meet specific applications.

In 1969, Hans Kelker succeeded in synthesizing a substance that had a nematic phase at room temperature, N-(4-methoxybenzylidene)-4-butylaniline (MBBA), which is one of the most popular subjects of liquid crystal research.George Gray.RRE Malvern), in 1973, led to design of new materials resulting in rapid adoption of small area LCDs within electronic products.

These molecules are rod-shaped, some created in the laboratory and some appearing spontaneously in nature. Since then, two new types of LC molecules have been synthesized: disc-shaped (by Sivaramakrishna Chandrasekhar in India in 1977)

In 1991, when liquid crystal displays were already well established, Pierre-Gilles de Gennes working at the Université Paris-Sud received the Nobel Prize in physics "for discovering that methods developed for studying order phenomena in simple systems can be generalized to more complex forms of matter, in particular to liquid crystals and polymers".

A large number of chemical compounds are known to exhibit one or several liquid crystalline phases. Despite significant differences in chemical composition, these molecules have some common features in chemical and physical properties. There are three types of thermotropic liquid crystals: discotic, conic (bowlic), and rod-shaped molecules. Discotics are disc-like molecules consisting of a flat core of adjacent aromatic rings, whereas the core in a conic LC is not flat, but is shaped like a rice bowl (a three-dimensional object).preferential alignment along one spatial direction.

A low melting point is preferable in order to avoid metastable, monotropic liquid crystalline phases. Low-temperature mesomorphic behavior in general is technologically more useful, and alkyl terminal groups promote this.

An extended, structurally rigid, highly anisotropic shape seems to be the main criterion for liquid crystalline behavior, and as a result many liquid crystalline materials are based on benzene rings.

The various liquid-crystal phases (called mesophases) can be characterized by the type of ordering. One can distinguish positional order (whether molecules are arranged in any sort of ordered lattice) and orientational order (whether molecules are mostly pointing in the same direction), and moreover order can be either short-range (only between molecules close to each other) or long-range (extending to larger, sometimes macroscopic, dimensions). Most thermotropic LCs will have an isotropic phase at high temperature. That is that heating will eventually drive them into a conventional liquid phase characterized by random and isotropic molecular ordering (little to no long-range order), and fluid-like flow behavior. Under other conditions (for instance, lower temperature), a LC might inhabit one or more phases with significant anisotropic orientational structure and short-range orientational order while still having an ability to flow.

The ordering of liquid crystalline phases is extensive on the molecular scale. This order extends up to the entire domain size, which may be on the order of micrometers, but usually does not extend to the macroscopic scale as often occurs in classical crystalline solids. However some techniques, such as the use of boundaries or an applied electric field, can be used to enforce a single ordered domain in a macroscopic liquid crystal sample. The orientational ordering in a liquid crystal might extend along only one dimension, with the material being essentially disordered in the other two directions.

Thermotropic phases are those that occur in a certain temperature range. If the temperature rise is too high, thermal motion will destroy the delicate cooperative ordering of the LC phase, pushing the material into a conventional isotropic liquid phase. At too low temperature, most LC materials will form a conventional crystal.mesogen) may exhibit various smectic phases followed by the nematic phase and finally the isotropic phase as temperature is increased. An example of a compound displaying thermotropic LC behavior is para-azoxyanisole.

Phase transition between a nematic (left) and smectic A (right) phases observed between crossed polarizers. The black color corresponds to isotropic medium.

The simplest liquid crystal phase is the nematic. In a nematic phase, calamitic organic molecules lack a crystalline positional order, but do self-align with their long axes roughly parallel. The molecules are free to flow and their center of mass positions are randomly distributed as in a liquid, but their orientation is constrained to form a long-range directional order.

Nematics also exhibit so-called "hedgehog" topological defects. In two dimensions, there are topological defects with topological charges +1/2 and -1/2. Due to hydrodynamics, the +1/2 defect moves considerably faster than the -1/2 defect. When placed close to each other, the defects attract; upon collision, they annihilate.

Most nematic phases are uniaxial: they have one axis (called a directrix) that is longer and preferred, with the other two being equivalent (can be approximated as cylinders or rods). However, some liquid crystals are biaxial nematic, meaning that in addition to orienting their long axis, they also orient along a secondary axis.liquid-crystal displays (LCD).

Nematic phases are also known in non-molecular systems: at high magnetic fields, electrons flow in bundles or stripes to create an "electronic nematic" form of matter.

Schematic of alignment in the smectic phases. The smectic A phase (left) has molecules organized into layers. In the smectic C phase (right), the molecules are tilted inside the layers

The smectic phases, which are found at lower temperatures than the nematic, form well-defined layers that can slide over one another in a manner similar to that of soap. The word "smectic" originates from the Latin word "smecticus", meaning cleaning, or having soap-like properties.p,p"-dinonylazobenzene.

Schematic of ordering in chiral liquid crystal phases. The chiral nematic phase (left), also called the cholesteric phase, and the smectic C* phase (right).

The chiral nematic phase exhibits chirality (handedness). This phase is often called the cholesteric phase because it was first observed for cholesterol derivatives. Only chiral molecules can give rise to such a phase. This phase exhibits a twisting of the molecules perpendicular to the director, with the molecular axis parallel to the director. The finite twist angle between adjacent molecules is due to their asymmetric packing, which results in longer-range chiral order. In the smectic C* phase (an asterisk denotes a chiral phase), the molecules have positional ordering in a layered structure (as in the other smectic phases), with the molecules tilted by a finite angle with respect to the layer normal. The chirality induces a finite azimuthal twist from one layer to the next, producing a spiral twisting of the molecular axis along the layer normal, hence they are also called twisted nematics.

The chiral pitch, p, refers to the distance over which the LC molecules undergo a full 360° twist (but note that the structure of the chiral nematic phase repeats itself every half-pitch, since in this phase directors at 0° and ±180° are equivalent). The pitch, p, typically changes when the temperature is altered or when other molecules are added to the LC host (an achiral LC host material will form a chiral phase if doped with a chiral material), allowing the pitch of a given material to be tuned accordingly. In some liquid crystal systems, the pitch is of the same order as the wavelength of visible light. This causes these systems to exhibit unique optical properties, such as Bragg reflection and low-threshold laser emission,elliptically polarized if it comes in obliquely.

A planar cell, filled with achiral LC host doped with an optically active Tröger base analog, placed between a pair of parallel (A) and crossed (B) linear polarizers. This doped mesogenic phase forms self-organized helical superstructures, that allow specific wavelengths of light pass through the crossed polarizers, and selectively reflects a particular wavelength of light.

Blue phases are liquid crystal phases that appear in the temperature range between a chiral nematic phase and an isotropic liquid phase. Blue phases have a regular three-dimensional cubic structure of defects with lattice periods of several hundred nanometers, and thus they exhibit selective Bragg reflections in the wavelength range of visible light corresponding to the cubic lattice. It was theoretically predicted in 1981 that these phases can possess icosahedral symmetry similar to quasicrystals.

Although blue phases are of interest for fast light modulators or tunable photonic crystals, they exist in a very narrow temperature range, usually less than a few kelvins. Recently the stabilization of blue phases over a temperature range of more than 60 K including room temperature (260–326 K) has been demonstrated.−4 s.blue phase mode LCD panel had been developed.

Blue phase crystals, being a periodic cubic structure with a bandgap in the visible wavelength range, can be considered as 3D photonic crystals. Producing ideal blue phase crystals in large volumes is still problematic, since the produced crystals are usually polycrystalline (platelet structure) or the single crystal size is limited (in the micrometer range). Recently, blue phases obtained as ideal 3D photonic crystals in large volumes have been stabilized and produced with different controlled crystal lattice orientations.

Conic LC molecules, like in discotics, can form columnar phases. Other phases, such as nonpolar nematic, polar nematic, stringbean, donut and onion phases, have been predicted. Conic phases, except nonpolar nematic, are polar phases.

Structure of lyotropic liquid crystal. The red heads of surfactant molecules are in contact with water, whereas the tails are immersed in oil (blue): bilayer (left) and micelle (right).

A lyotropic liquid crystal consists of two or more components that exhibit liquid-crystalline properties in certain concentration ranges. In the lyotropic phases, solvent molecules fill the space around the compounds to provide fluidity to the system.

A compound that has two immiscible hydrophilic and hydrophobic parts within the same molecule is called an amphiphilic molecule. Many amphiphilic molecules show lyotropic liquid-crystalline phase sequences depending on the volume balances between the hydrophilic part and hydrophobic part. These structures are formed through the micro-phase segregation of two incompatible components on a nanometer scale. Soap is an everyday example of a lyotropic liquid crystal.

The content of water or other solvent molecules changes the self-assembled structures. At very low amphiphile concentration, the molecules will be dispersed randomly without any ordering. At slightly higher (but still low) concentration, amphiphilic molecules will spontaneously assemble into micelles or vesicles. This is done so as to "hide" the hydrophobic tail of the amphiphile inside the micelle core, exposing a hydrophilic (water-soluble) surface to aqueous solution. These spherical objects do not order themselves in solution, however. At higher concentration, the assemblies will become ordered. A typical phase is a hexagonal columnar phase, where the amphiphiles form long cylinders (again with a hydrophilic surface) that arrange themselves into a roughly hexagonal lattice. This is called the middle soap phase. At still higher concentration, a lamellar phase (neat soap phase) may form, wherein extended sheets of amphiphiles are separated by thin layers of water. For some systems, a cubic (also called viscous isotropic) phase may exist between the hexagonal and lamellar phases, wherein spheres are formed that create a dense cubic lattice. These spheres may also be connected to one another, forming a bicontinuous cubic phase.

The objects created by amphiphiles are usually spherical (as in the case of micelles), but may also be disc-like (bicelles), rod-like, or biaxial (all three micelle axes are distinct). These anisotropic self-assembled nano-structures can then order themselves in much the same way as thermotropic liquid crystals do, forming large-scale versions of all the thermotropic phases (such as a nematic phase of rod-shaped micelles).

For some systems, at high concentrations, inverse phases are observed. That is, one may generate an inverse hexagonal columnar phase (columns of water encapsulated by amphiphiles) or an inverse micellar phase (a bulk liquid crystal sample with spherical water cavities).

Even within the same phases, their self-assembled structures are tunable by the concentration: for example, in lamellar phases, the layer distances increase with the solvent volume. Since lyotropic liquid crystals rely on a subtle balance of intermolecular interactions, it is more difficult to analyze their structures and properties than those of thermotropic liquid crystals.

Liquid crystal phases can also be based on low-melting inorganic phases like ZnCl2 that have a structure formed of linked tetrahedra and easily form glasses. The addition of long chain soap-like molecules leads to a series of new phases that show a variety of liquid crystalline behavior both as a function of the inorganic-organic composition ratio and of temperature. This class of materials has been named metallotropic.

Thermotropic mesophases are detected and characterized by two major methods, the original method was use of thermal optical microscopy,differential scanning calorimetry (DSC),

Lyotropic mesophases are analyzed in a similar fashion, though these experiments are somewhat more complex, as the concentration of mesogen is a key factor. These experiments are run at various concentrations of mesogen in order to analyze that impact.

Lyotropic liquid-crystalline phases are abundant in living systems, the study of which is referred to as lipid polymorphism. Accordingly, lyotropic liquid crystals attract particular attention in the field of biomimetic chemistry. In particular, biological membranes and cell membranes are a form of liquid crystal. Their constituent molecules (e.g. phospholipids) are perpendicular to the membrane surface, yet the membrane is flexible. These lipids vary in shape (see page on lipid polymorphism). The constituent molecules can inter-mingle easily, but tend not to leave the membrane due to the high energy requirement of this process. Lipid molecules can flip from one side of the membrane to the other, this process being catalyzed by flippases and floppases (depending on the direction of movement). These liquid crystal membrane phases can also host important proteins such as receptors freely "floating" inside, or partly outside, the membrane, e.g. CTP:phosphocholine cytidylyltransferase (CCT).

Many other biological structures exhibit liquid-crystal behavior. For instance, the concentrated protein solution that is extruded by a spider to generate silk is, in fact, a liquid crystal phase. The precise ordering of molecules in silk is critical to its renowned strength. DNA and many polypeptides, including actively-driven cytoskeletal filaments,

Examples of liquid crystals can also be found in the mineral world, most of them being lyotropic. The first discovered was vanadium(V) oxide, by Zocher in 1925.nematic phase in the case of the smectite clays family was raised by Langmuir in 1938,

With the rapid development of nanosciences, and the synthesis of many new anisotropic nanoparticles, the number of such mineral liquid crystals is increasing quickly, with, for example, carbon nanotubes and graphene. A lamellar phase was even discovered, H3Sb3P2O14, which exhibits hyperswelling up to ~250 nm for the interlamellar distance.

Anisotropy of liquid crystals is a property not observed in other fluids. This anisotropy makes flows of liquid crystals behave more differentially than those of ordinary fluids. For example, injection of a flux of a liquid crystal between two close parallel plates (viscous fingering) causes orientation of the molecules to couple with the flow, with the resulting emergence of dendritic patterns.surface tension) between different liquid crystal phases. This anisotropy determines the equilibrium shape at the coexistence temperature, and is so strong that usually facets appear. When temperature is changed one of the phases grows, forming different morphologies depending on the temperature change.

Microscopic theoretical treatment of fluid phases can become quite complicated, owing to the high material density, meaning that strong interactions, hard-core repulsions, and many-body correlations cannot be ignored. In the case of liquid crystals, anisotropy in all of these interactions further complicates analysis. There are a number of fairly simple theories, however, that can at least predict the general behavior of the phase transitions in liquid crystal systems.

As we already saw above, the nematic liquid crystals are composed of rod-like molecules with the long axes of neighboring molecules aligned approximately to one another. To describe this anisotropic structure, a dimensionless unit vector n called the director, is introduced to represent the direction of preferred orientation of molecules in the neighborhood of any point. Because there is no physical polarity along the director axis, n and -n are fully equivalent.

The order of a liquid crystal could also be characterized by using other even Legendre polynomials (all the odd polynomials average to zero since the director can point in either of two antiparallel directions). These higher-order averages are more difficult to measure, but can yield additional information about molecular ordering.

A positional order parameter is also used to describe the ordering of a liquid crystal. It is characterized by the variation of the density of the center of mass of the liquid crystal molecules along a given vector. In the case of positional variation along the z-axis the density ρ

A simple model which predicts lyotropic phase transitions is the hard-rod model proposed by Lars Onsager. This theory considers the volume excluded from the center-of-mass of one idealized cylinder as it approaches another. Specifically, if the cylinders are oriented parallel to one another, there is very little volume that is excluded from the center-of-mass of the approaching cylinder (it can come quite close to the other cylinder). If, however, the cylinders are at some angle to one another, then there is a large volume surrounding the cylinder which the approaching cylinder"s center-of-mass cannot enter (due to the hard-rod repulsion between the two idealized objects). Thus, this angular arrangement sees a decrease in the net positional entropy of the approaching cylinder (there are fewer states available to it).

The fundamental insight here is that, whilst parallel arrangements of anisotropic objects lead to a decrease in orientational entropy, there is an increase in positional entropy. Thus in some case greater positional order will be entropically favorable. This theory thus predicts that a solution of rod-shaped objects will undergo a phase transition, at sufficient concentration, into a nematic phase. Although this model is conceptually helpful, its mathematical formulation makes several assumptions that limit its applicability to real systems.

This statistical theory, proposed by Alfred Saupe and Wilhelm Maier, includes contributions from an attractive intermolecular potential from an induced dipole moment between adjacent rod-like liquid crystal molecules. The anisotropic attraction stabilizes parallel alignment of neighboring molecules, and the theory then considers a mean-field average of the interaction. Solved self-consistently, this theory predicts thermotropic nematic-isotropic phase transitions, consistent with experiment.bending stiffness of the molecules and using the method of path integrals in polymer science.

{\displaystyle \sigma =\left\langle \cos \left({\frac {2\pi z_{i}}{d}}\right)\left({\frac {3}{2}}\cos ^{2}\left(\theta _{i}\right)-{\frac {1}{2}}\right)\right\rangle }

The values zi, θi, and d are the position of the molecule, the angle between the molecular axis and director, and the layer spacing. The postulated potential energy of a single molecule is given by:

{\displaystyle U_{i}(\theta _{i},z_{i})=-U_{0}\left(S+\alpha \sigma \cos \left({\frac {2\pi z_{i}}{d}}\right)\right)\left({\frac {3}{2}}\cos ^{2}\left(\theta _{i}\right)-{\frac {1}{2}}\right)}

Here constant α quantifies the strength of the interaction between adjacent molecules. The potential is then used to derive the thermodynamic properties of the system assuming thermal equilibrium. It results in two self-consistency equations that must be solved numerically, the solutions of which are the three stable phases of the liquid crystal.

In this formalism, a liquid crystal material is treated as a continuum; molecular details are entirely ignored. Rather, this theory considers perturbations to a presumed oriented sample. The distortions of the liquid crystal are commonly described by the Frank free energy density. One can identify three types of distortions that could occur in an oriented sample: (1) twists of the material, where neighboring molecules are forced to be angled with respect to one another, rather than aligned; (2) splay of the material, where bending occurs perpendicular to the director; and (3) bend of the material, where the distortion is parallel to the director and molecular axis. All three of these types of distortions incur an energy penalty. They are distortions that are induced by the boundary conditions at domain walls or the enclosing container. The response of the material can then be decomposed into terms based on the elastic constants corresponding to the three types of distortions. Elastic continuum theory is an effective tool for modeling liquid crystal devices and lipid bilayers.

Scientists and engineers are able to use liquid crystals in a variety of applications because external perturbation can cause significant changes in the macroscopic properties of the liquid crystal system. Both electric and magnetic fields can be used to induce these changes. The magnitude of the fields, as well as the speed at which the molecules align are important characteristics industry deals with. Special surface treatments can be used in liquid crystal devices to force specific orientations of the director.

The ability of the director to align along an external field is caused by the electric nature of the molecules. Permanent electric dipoles result when one end of a molecule has a net positive charge while the other end has a net negative charge. When an external electric field is applied to the liquid crystal, the dipole molecules tend to orient themselves along the direction of the field.

Even if a molecule does not form a permanent dipole, it can still be influenced by an electric field. In some cases, the field produces slight re-arrangement of electrons and protons in molecules such that an induced electric dipole results. While not as strong as permanent dipoles, orientation with the external field still occurs.

The effects of magnetic fields on liquid crystal molecules are analogous to electric fields. Because magnetic fields are generated by moving electric charges, permanent magnetic dipoles are produced by electrons moving about atoms. When a magnetic field is applied, the molecules will tend to align with or against the field. Electromagnetic radiation, e.g. UV-Visible light, can influence light-responsive liquid crystals which mainly carry at least a photo-switchable unit.

In the absence of an external field, the director of a liquid crystal is free to point in any direction. It is possible, however, to force the director to point in a specific direction by introducing an outside agent to the system. For example, when a thin polymer coating (usually a polyimide) is spread on a glass substrate and rubbed in a single direction with a cloth, it is observed that liquid crystal molecules in contact with that surface align with the rubbing direction. The currently accepted mechanism for this is believed to be an epitaxial growth of the liquid crystal layers on the partially aligned polymer chains in the near surface layers of the polyimide.

Several liquid crystal chemicals also align to a "command surface" which is in turn aligned by electric field of polarized light. This process is called photoalignment.

The competition between orientation produced by surface anchoring and by electric field effects is often exploited in liquid crystal devices. Consider the case in which liquid crystal molecules are aligned parallel to the surface and an electric field is applied perpendicular to the cell. At first, as the electric field increases in magnitude, no change in alignment occurs. However at a threshold magnitude of electric field, deformation occurs. Deformation occurs where the director changes its orientation from one molecule to the next. The occurrence of such a change from an aligned to a deformed state is called a Fredericks transition and can also be produced by the application of a magnetic field of sufficient strength.

The Fredericks transition is fundamental to the operation of many liquid crystal displays because the director orientation (and thus the properties) can be controlled easily by the application of a field.

As already described, chiral liquid-crystal molecules usually give rise to chiral mesophases. This means that the molecule must possess some form of asymmetry, usually a stereogenic center. An additional requirement is that the system not be racemic: a mixture of right- and left-handed molecules will cancel the chiral effect. Due to the cooperative nature of liquid crystal ordering, however, a small amount of chiral dopant in an otherwise achiral mesophase is often enough to select out one domain handedness, making the system overall chiral.

Chiral phases usually have a helical twisting of the molecules. If the pitch of this twist is on the order of the wavelength of visible light, then interesting optical interference effects can be observed. The chiral twisting that occurs in chiral LC phases also makes the system respond differently from right- and left-handed circularly polarized light. These materials can thus be used as polarization filters.

It is possible for chiral LC molecules to produce essentially achiral mesophases. For instance, in certain ranges of concentration and molecular weight, DNA will form an achiral line hexatic phase. An interesting recent observation is of the formation of chiral mesophases from achiral LC molecules. Specifically, bent-core molecules (sometimes called banana liquid crystals) have been shown to form liquid crystal phases that are chiral.ferroelectric or anti-ferroelectric, both of which are of interest for applications.

Chirality can also be incorporated into a phase by adding a chiral dopant, which may not form LCs itself. Twisted-nematic or super-twisted nematic mixtures often contain a small amount of such dopants.

Structure of liquid crystal display: 1 – vertical polarization filter, 2, 4 – glass with electrodes, 3 – liquid crystals, 5 – horizontal polarization filter, 6 – reflector

Liquid crystals find wide use in liquid crystal displays, which rely on the optical properties of certain liquid crystalline substances in the presence or absence of an electric field. In a typical device, a liquid crystal layer (typically 4 μm thick) sits between two polarizers that are crossed (oriented at 90° to one another). The liquid crystal alignment is chosen so that its relaxed phase is a twisted one (see Twisted nematic field effect).

Thermotropic chiral LCs whose pitch varies strongly with temperature can be used as crude liquid crystal thermometers, since the color of the material will change as the pitch is changed. Liquid crystal color transitions are used on many aquarium and pool thermometers as well as on thermometers for infants or baths.failure analysis in the semiconductor industry.

Liquid crystal lenses converge or diverge the incident light by adjusting the refractive index of liquid crystal layer with applied voltage or temperature. Generally, the liquid crystal lenses generate a parabolic refractive index distribution by arranging molecular orientations. Therefore, a plane wave is reshaped into a parabolic wavefront by a liquid crystal lens. The focal length of liquid crystal lenses could be continuously tunable when the external electric field can be properly tuned. Liquid crystal lenses are a kind of adaptive optics. Imaging system can be benefited with focusing correction, image plane adjustment, or changing the range of depth-of-field or depth of focus. Liquid crystal lens is one of the candidates to develop vision correction device for myopia and presbyopia eyes (e.g., tunable eyeglass and smart contact lenses).phase modulator, a liquid crystal lens feature space-variant optical path length (i.e., optical path length as the function of its pupil coordinate). In different imaging system, the required function of optical path length varies from one to another. For example, to converge a plane wave into a diffraction limited spot, for a physically-planar liquid crystal structure, the refractive index of liquid crystal layer should be spherical or paraboloidal under paraxial approximation. As for projecting images or sensing objects, it may be expected to have the liquid crystal lens with aspheric distribution of optical path length across its aperture of interest. Liquid crystal lenses with electrically tunable refractive index (by addressing the different magnitude of electric field on liquid crystal layer) have potentials to achieve arbitrary function of optical path length for modulating incoming wavefront; current liquid crystal freeform optical elements were extended from liquid crystal lens with same optical mechanisms.

Liquid crystal lasers use a liquid crystal in the lasing medium as a distributed feedback mechanism instead of external mirrors. Emission at a photonic bandgap created by the periodic dielectric structure of the liquid crystal gives a low-threshold high-output device with stable monochromatic emission.

Polymer dispersed liquid crystal (PDLC) sheets and rolls are available as adhesive backed Smart film which can be applied to windows and electrically switched between transparent and opaque to provide privacy.

Liquid crystal films have revolutionized the world of technology. Currently they are used in the most diverse devices, such as digital clocks, mobile phones, calculating machines and televisions. The use of liquid crystal films in optical memory devices, with a process similar to the recording and reading of CDs and DVDs may be possible.

Liquid crystals are also used as basic technology to imitate quantum computers, using electric fields to manipulate the orientation of the liquid crystal molecules, to store data and to encode a different value for every different degree of misalignment with other molecules.

Castellano JA (2005). Liquid Gold: The Story of Liquid Crystal Displays and the Creation of an Industry. World Scientific Publishing. ISBN 978-981-238-956-5.

Gray GW, Harrison KJ, Nash JA (1973). "New family of nematic liquid crystals for displays". Electronics Letters. 9 (6): 130. Bibcode:1973ElL.....9..130G. doi:10.1049/el:19730096.

Chandrasekhar S, Sadashiva BK, Suresh KA (1977). "Liquid crystals of disc-like molecules". Pramana. 9 (5): 471–480. Bibcode:1977Prama...9..471C. doi:10.1007/bf02846252. S2CID 98207805.

Lam L (1994). "Bowlics". In Shibaev VP, Lam L (eds.). Liquid Crystalline and Mesomorphic Polymers. Partially Ordered Systems. New York: Springer. pp. 324–353. doi:10.1007/978-1-4613-8333-8_10. ISBN 978-1-4613-8333-8.

Shao Y, Zerda TW (1998). "Phase Transitions of Liquid Crystal PAA in Confined Geometries". Journal of Physical Chemistry B. 102 (18): 3387–3394. doi:10.1021/jp9734437.

Géza T, Denniston C, Yeomans JM (February 26, 2002). "Hydrodynamics of Topological Defects in Nematic Liquid Crystals". Physical Review Letters. 88 (10): 105504. arXiv:Bibcode:2002PhRvL..88j5504T. doi:10.1103/PhysRevLett.88.105504. PMID 11909370. S2CID 38594358.

Géza T, Denniston C, Yeomans JM (May 21, 2003). "Hydrodynamics of domain growth in nematic liquid crystals". Physical Review E. 67 (5): 051705. arXiv:Bibcode:2003PhRvE..67e1705T. doi:10.1103/PhysRevE.67.051705. PMID 12786162. S2CID 13796254.

Davidson P, Penisson C, Constantin D, Gabriel JP (June 2018). "Isotropic, nematic, and lamellar phases in colloidal suspensions of nanosheets". Proceedings of the National Academy of Sciences of the United States of America. 115 (26): 6662–6667. Bibcode:2018PNAS..115.6662D. doi:PMC PMID 29891691.

Kopp VI, Fan B, Vithana HK, Genack AZ (November 1998). "Low-threshold lasing at the edge of a photonic stop band in cholesteric liquid crystals". Optics Letters. 23 (21): 1707–9. Bibcode:1998OptL...23.1707K. doi:10.1364/OL.23.001707. PMID 18091891.

Kazem-Rostami M (2019). "Optically active and photoswitchable Tröger"s base analogs". New Journal of Chemistry. 43 (20): 7751–7755. doi:10.1039/C9NJ01372E. S2CID 164362391.

Yamamoto J, Nishiyama I, Inoue M, Yokoyama H (September 2005). "Optical isotropy and iridescence in a smectic "blue phase"". Nature. 437 (7058): 525–8. Bibcode:2005Natur.437..525Y. doi:10.1038/nature04034. PMID 16177785. S2CID 4432184.

Wang L, Huang D, Lam L, Cheng Z (2017). "Bowlics: history, advances and applications". Liquid Crystals Today. 26 (4): 85–111. doi:10.1080/1358314X.2017.1398307. S2CID 126256863.

Liang Q, Liu P, Liu C, Jian X, Hong D, Li Y (2005). "Synthesis and Properties of Lyotropic Liquid Crystalline Copolyamides Containing Phthalazinone Moieties and Ether Linkages". Polymer. 46 (16): 6258–6265. doi:10.1016/j.polymer.2005.05.059.

Martin JD, Keary CL, Thornton TA, Novotnak MP, Knutson JW, Folmer JC (April 2006). "Metallotropic liquid crystals formed by surfactant templating of molten metal halides". Nature Materials. 5 (4): 271–5. Bibcode:2006NatMa...5..271M. doi:10.1038/nmat1610. PMID 16547520. S2CID 35833273.

Tomczyk W, Marzec M, Juszyńska-Gałązka E, Węgłowska D (2017). "Mesomorphic and physicochemical properties of liquid crystal mixture composed of chiral molecules with perfluorinated terminal chains". Journal of Molecular Structure. 1130: 503–510. Bibcode:2017JMoSt1130..503T. doi:10.1016/j.molstruc.2016.10.039.

Juszyńska-Gałązka E, Gałązka M, Massalska-Arodź M, Bąk A, Chłędowska K, Tomczyk W (December 2014). "Phase Behavior and Dynamics of the Liquid Crystal 4"-butyl-4-(2-methylbutoxy)azoxybenzene (4ABO5*)". The Journal of Physical Chemistry B. 118 (51): 14982–9. doi:10.1021/jp510584w. PMID 25429851.

Wensink HH, Dunkel J, Heidenreich S, Drescher K, Goldstein RE, Löwen H, Yeomans JM (September 2012). "Meso-scale turbulence in living fluids". Proceedings of the National Academy of Sciences of the United States of America. 109 (36): 14308–13. Bibcode:2013PNAS..110.4488S. doi:PMC PMID 22908244.

Langmuir I (1938). "The role of attractive and repulsive forces in the formation of tactoids, thixotropic gels, protein crystals and coacervates". J Chem Phys. 6 (12): 873. Bibcode:1938JChPh...6..873L. doi:10.1063/1.1750183.

Gabriel JC, Sanchez C, Davidson P (1996). "Observation of Nematic Liquid-Crystal Textures in Aqueous Gels of Smectite Clays". J. Phys. Chem. 100 (26): 11139. doi:10.1021/jp961088z.

Paineau E, Philippe AM, Antonova K, Bihannic I, Davidson P, Dozov I, et al. (2013). "Liquid–crystalline properties of aqueous suspensions of natural clay nanosheets". Liquid Crystals Reviews. 1 (2): 110. doi:10.1080/21680396.2013.842130. S2CID 136533412.

González-Cinca R, Ramirez-Piscina L, Casademunt J, Hernández-Machado A, Kramer L, Katona TT, et al. (1996). "Phase-field simulations and experiments of faceted growth in liquid crystal". Physica D. 99 (2–3): 359. Bibcode:1996PhyD...99..359G. doi:10.1016/S0167-2789(96)00162-5.

González-Cinca R, Ramırez-Piscina L, Casademunt J, Hernández-Machado A, Tóth-Katona T, Börzsönyi T, Buka Á (1998). "Heat diffusion anisotropy in dendritic growth: phase field simulations and experiments in liquid crystals". Journal of Crystal Growth. 193 (4): 712. Bibcode:1998JCrGr.193..712G. doi:10.1016/S0022-0248(98)00505-3.

Onsager L (1949). "The effects of shape on the interaction of colloidal particles". Annals of the New York Academy of Sciences. 51 (4): 627. Bibcode:1949NYASA..51..627O. doi:10.1111/j.1749-6632.1949.tb27296.x. S2CID 84562683.

Maier W, Saupe A (1958). "Eine einfache molekulare theorie des nematischen kristallinflussigen zustandes". Z. Naturforsch. A (in German). 13 (7): 564. Bibcode:1958ZNatA..13..564M. doi:10.1515/zna-1958-0716. S2CID 93402217.

McMillan W (1971). "Simple Molecular Model for the Smectic A Phase of Liquid Crystals". Phys. Rev. A. 4 (3): 1238. Bibcode:1971PhRvA...4.1238M. doi:10.1103/PhysRevA.4.1238.

Leslie FM (1992). "Continuum theory for nematic liquid crystals". Continuum Mechanics and Thermodynamics. 4 (3): 167. Bibcode:1992CMT.....4..167L. doi:10.1007/BF01130288. S2CID 120908851.

Watson MC, Brandt EG, Welch PM, Brown FL (July 2012). "Determining biomembrane bending rigidities from simulations of modest size". Physical Review Letters. 109 (2): 028102. Bibcode:2012PhRvL.109b8102W. doi:10.1103/PhysRevLett.109.028102. PMID 23030207.

Achard MF, Bedel JP, Marcerou JP, Nguyen HT, Rouillon JC (February 2003). "Switching of banana liquid crystal mesophases under field". The European Physical Journal E. 10 (2): 129–34. Bibcode:2003EPJE...10..129A. doi:10.1140/epje/e2003-00016-y. PMID 15011066. S2CID 35942754.

Uehara H, Hatano J (2002). "Pressure-Temperature Phase Diagrams of Ferroelectric Liquid Crystals". J. Phys. Soc. Jpn. 71 (2): 509. Bibcode:2002JPSJ...71..509U. doi:10.1143/JPSJ.71.509.

Alkeskjold TT, Scolari L, Noordegraaf D, Lægsgaard J, Weirich J, Wei L, Tartarini G, Bassi P, Gauza S, Wu S, Bjarklev A (2007). "Integrating liquid crystal based optical devices in photonic crystal". Optical and Quantum Electronics. 39 (12–13): 1009. doi:10.1007/s11082-007-9139-8. S2CID 54208691.

Sato S (1979). "Liquid-Crystal Lens-Cells with Variable Focal Length". Japanese Journal of Applied Physics. 18 (9): 1679–1684. Bibcode:1979JaJAP..18.1679S. doi:10.1143/JJAP.18.1679. S2CID 119784753.

Dolgaleva K, Wei SK, Lukishova SG, Chen SH, Schwertz K, Boyd RW (2008). "Enhanced laser performance of cholesteric liquid crystals doped with oligofluorene dye". Journal of the Optical Society of America. 25 (9): 1496–1504. Bibcode:2008JOSAB..25.1496D. doi:10.1364/JOSAB.25.001496.

Luzzati V, Mustacchi H, Skoulios A (1957). "Structure of the Liquid-Crystal Phases of the Soap–water System: Middle Soap and Neat Soap". Nature. 180 (4586): 600. Bibcode:1957Natur.180..600L. doi:10.1038/180600a0. S2CID 4163714.

Silva MC, Sotomayor J, Figueirinhas J (September 2015). "Effect of an additive on the permanent memory effect of polymer dispersed liquid crystal films". Journal of Chemical Technology & Biotechnology. 90 (9): 1565–9. doi:10.1002/jctb.4677.

da Silva MC, Figue